Question

已知函數f（x）=x³+ax+b的圖象是曲線C，直線y=kx+1與曲線C相切于點（1，3）．
（I）求函數f（x）的解析式；
（II）求函數f（x）的遞增區間；
（III）求函數F（x）=f（x）-2x-3在區間[0，2]上的最大值和最小值．

Answer 1

分析：（I）先通過切點，求出k的值；再利用f（x）的導函數和切點求出a，b的值．最后代入即可得f（x）的解析式．
（II）通過在函數的單調遞增區間，函數f（x）的導函數大于零，求出x的取值范圍．
（III）通過函數F（x）的導函數F'（x）=0，求出函數的極值．列出x，F'（x），F（x）關系表，通過觀察可知F（x）在區間[0，2]最大和最小值．

解答：解：（I）∵切點為（1，3），∴k+1=3，得k=2．
∵f'（x）=3x²+a，
∴f'（1）=3+a=2，得a=-1．
則f（x）=x³-x+b．
由f（1）=3得b=3．
∴f（x）=x³-x+3．

（II）由f（x）=x³-x+3得f'（x）=3x²-1，
令f'（x）=3x²-1＞0，解得x＜-

3

3

或x＞

3

3

∴函數f（x）的增區間為(-∞，-

3

3

)，(

3

3

，+∞)．
（III）F（x）=x³-3x，F'（x）=3x²-3
令F'（x）=3x²-3=0，得x₁=-1，x₂=1．
列出x，F'（x），F（x）關系如下：

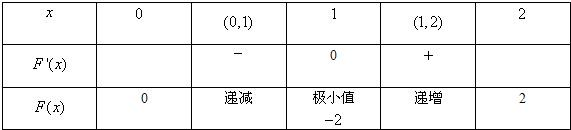
∴當x∈[0，2]時，F（x）的最大值為2，最小值為-2．

點評：本題主要考查了用待定系數法求函數的解析式．解此類題常用到導函數與函數的關系來解決問題．