解:(1)如圖,設M(x
1,y
1),N(x
2,y
2)
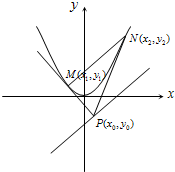
由y=
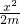
,得y′=
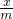
,∴PM的斜率為
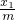
,PM的方程為y=
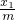
x-y
1
同理得PN:y=
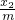
x-y
2,
設P(x
0,y
0)代入上式得 y
0=
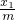
x
0-y
1,y
0=
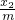
x
0-y
2,
即(x
1,y
1),(x
2,y
2)滿足方程y
0=
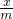
x
0-y
故MN的方程為y=
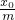
x-y
0=
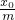
x-(x
0-m)
上式可化為y-m=
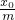
(x-m),過交點(m,m)
∵MN過交點Q(1,1),
∴m=1
∴拋物線C的方程為x
2=2y
(2)設A(x
3,y
3),B(x
4,y
4)
則
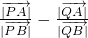
=
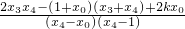
…(Ⅰ)
∵P(x
0,y
0),Q(1,1)
∴PQ直線方程為y-1=
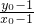
(x-1),
與x
2=2y聯立化簡x
2-
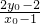
x+
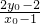
-2=0
∴x
3x
4=
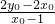
…①,x
3+x
4=
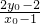
…②
把①②代入(Ⅰ)式中,
則分子2x
3x
4-(1+x
0)(x
3+x
4)+2kx
0=
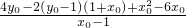
…(Ⅱ)
又P點在直線y=kx-1上,
∴y
0=kx
0-1代入(Ⅱ)中得:2x
3x
4-(1+x
0)(x
3+x
4)+2kx
0=0
∴
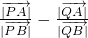
=
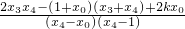
=0
分析:(1)對C的函數求導數,設出兩個切點的坐標,求出導函數在切點處的導數值即切線的斜率,利用點斜式寫出切線
PM,PN 的方程,將P的坐標代入得到MN的方程,據直線的點斜式判斷出MN過的定點,據已知求出拋物線C的方程.
(2)設出直線PQ的方程,將直線方程與拋物線方程聯立,利用韋達定理得解.
點評:解決直線與圓錐曲線的位置關系問題,一般是設出直線方程,將直線方程與圓錐曲線方程聯立,消去一個未知數,得到關于一個未知數的二次方程,然后利用韋達定理找突破口.

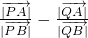 的值.
的值.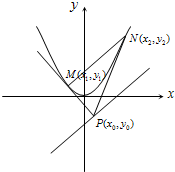
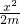 ,得y′=
,得y′=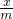 ,∴PM的斜率為
,∴PM的斜率為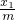 ,PM的方程為y=
,PM的方程為y=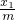 x-y1
x-y1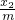 x-y2,
x-y2,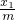 x0-y1,y0=
x0-y1,y0=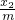 x0-y2,
x0-y2,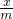 x0-y
x0-y 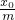 x-y0=
x-y0=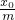 x-(x0-m)
x-(x0-m)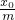 (x-m),過交點(m,m)
(x-m),過交點(m,m)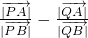 =
=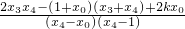 …(Ⅰ)
…(Ⅰ)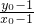 (x-1),
(x-1),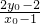 x+
x+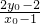 -2=0
-2=0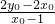 …①,x3+x4=
…①,x3+x4=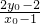 …②
…②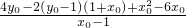 …(Ⅱ)
…(Ⅱ)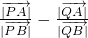 =
=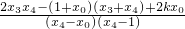 =0
=0
