【題目】已知數列
滿足對
時，
，其對
，有
，則數列
的前50項的和為__________．
【答案】
【解析】分析：由題意可得數列的前幾項，可得數列{an}為周期為4的數列，且以1，2，3，2反復出現，運用等差數列的求和公式，計算可得所求和．
詳解: 數列{an}滿足對1≤n≤3時，an=n，且對n∈N*，有an+3+an+1=an+2+an，
可得a1=1，a2=2，a3=3，a4=1+3﹣2=2，
a5=2+2﹣3=1，a6=2，a7=3，a8=2，a9=1，a10=2，…，
則數列{an}為周期為4的數列，且以1，2，3，2反復出現，
可得數列{nan}的前50項的和為
（1+5+…+49）+2（2+6+…+50）+3（3+7+…+47）+2（4+8+…+48）
=
×（1+49）×13+2××（2+50）×13+3×（3+47）×12+2×（4+48）×12
=2525．
故答案為：2525．
科目：高中數學 來源： 題型：
【題目】如圖，AB是圓O的直徑，PA垂直于圓O所在的平面，M是圓周上任意一點，AN⊥PM，垂足為N , AE⊥PB，垂足為E .
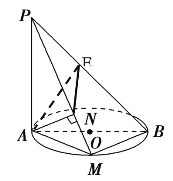
（1）求證：平面PAM⊥平面PBM.
（2）求證：
是二面角A-PB-M的平面角.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某投資公司計劃投資A，B兩種金融產品，根據市場調查與預測，A產品的利潤
與投資金額x的函數關系為
，B產品的利潤
與投資金額x的函數關系為
．（利潤與投資金額單位：萬元）
（1）該公司已有100萬元資金，并全部投入A，B兩種產品中，其中x萬元資金投入A產品，試把A，B兩種產品利潤總和表示為x的函數，并寫出x的取值范圍．
（2）怎樣分配這100萬元資金，才能使公司獲得最大利潤？其最大利潤為多少萬元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】 設函數f(x)＝(x－1)2＋bln x，其中b為常數．
(1)當b>
時，判斷函數f(x)在定義域上的單調性；
(2)若函數f(x)有極值點，求b的取值范圍及f(x)的極值點．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P－ABCD中，底面ABCD為菱形，∠BAD＝60°，Q為AD的中點．
(1)若PA＝PD，求證：平面PQB⊥平面PAD；
(2)點M在線段PC上，PM＝tPC，試確定實數t的值，使得PA∥平面MQB.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用二分法求函數
的一個正零點的近似值（精確度為0.1）時，依次計算得到如下數據：f（1）＝–2，f（1.5）＝0.625，f（1.25）≈–0.984，f（1.375）≈–0.260，關于下一步的說法正確的是（ ）
A. 已經達到精確度的要求，可以取1.4作為近似值
B. 已經達到精確度的要求，可以取1.375作為近似值
C. 沒有達到精確度的要求，應該接著計算f（1.4375）
D. 沒有達到精確度的要求，應該接著計算f（1.3125）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
