


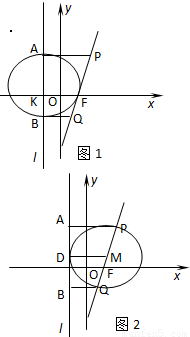
 解:(Ⅰ)過F作l的垂線交l于K,以KF的中點為原點,KF所在直線為x軸建立平面直角坐標系如圖1,
解:(Ⅰ)過F作l的垂線交l于K,以KF的中點為原點,KF所在直線為x軸建立平面直角坐標系如圖1, .
. ,∴
,∴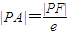 ,同理得
,同理得 .
. ,
, ,∴
,∴ ,同理得
,同理得 .
. ,
,

 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
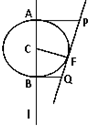
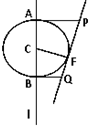 (2007•湛江二模)如圖,F是定直線l外的一個定點,C是l上的動點,有下列結論:若以C為圓心,CF為半徑的圓與l相交于A、B兩點,過A、B分別作l的垂線與圓C過F的切線相交于點P和點Q,則必在以F為焦點,l為準線的同一條拋物線上.
(2007•湛江二模)如圖,F是定直線l外的一個定點,C是l上的動點,有下列結論:若以C為圓心,CF為半徑的圓與l相交于A、B兩點,過A、B分別作l的垂線與圓C過F的切線相交于點P和點Q,則必在以F為焦點,l為準線的同一條拋物線上.查看答案和解析>>
科目:高中數學 來源: 題型:
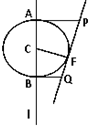
 如圖,F是定直線l外的一個定點,C是l上的動點,有下列結論:若以C為圓心,CF為半徑的圓與l交于A、B兩點,過A、B分別作l的垂線與圓
如圖,F是定直線l外的一個定點,C是l上的動點,有下列結論:若以C為圓心,CF為半徑的圓與l交于A、B兩點,過A、B分別作l的垂線與圓
C過F的切線交于點P和點Q,則P、Q必在以F為焦點,l為準線的同一條拋物線上.
(Ⅰ)建立適當的坐標系,求出該拋物線的方程;
(Ⅱ)對以上結論的反向思考可以得到另一個命題:
“若過拋物線焦點F的直線與拋物線交于P、Q兩點,
則以PQ為直徑的圓一定與拋物線的準線l相切”請
問:此命題是否正確?試證明你的判斷;
(Ⅲ)請選擇橢圓或雙曲線之一類比(Ⅱ)寫出相應的命題并
證明其真假.(只選擇一種曲線解答即可,若兩種都選,則以第一選擇為評分依據)
查看答案和解析>>
科目:高中數學 來源:湛江二模 題型:解答題
查看答案和解析>>
科目:高中數學 來源:湛江二模 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com