
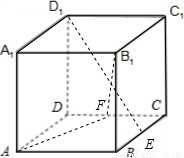
 如圖,在棱長為1的正方體ABCD-A1B1C1D1中,點(diǎn)E是棱BC的中點(diǎn),點(diǎn)F是棱CD上的動(dòng)點(diǎn).
如圖,在棱長為1的正方體ABCD-A1B1C1D1中,點(diǎn)E是棱BC的中點(diǎn),點(diǎn)F是棱CD上的動(dòng)點(diǎn).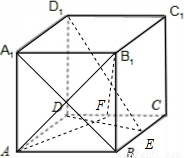 解法一:(I)連接A1B,則A1B是D1E在面ABB1A;內(nèi)的射影
解法一:(I)連接A1B,則A1B是D1E在面ABB1A;內(nèi)的射影 AC=
AC=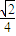 ,
, .
.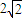 ,從而∠AHC1=π-arctan2
,從而∠AHC1=π-arctan2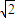 .
.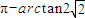 .
.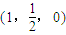 ,F(xiàn)(x,1,0)∴
,F(xiàn)(x,1,0)∴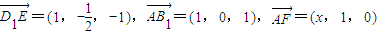
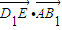 =1-1=0,即D1E⊥AB1
=1-1=0,即D1E⊥AB1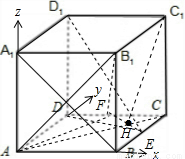
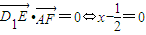
 .故當(dāng)點(diǎn)F是CD的中點(diǎn)時(shí),D1E⊥平面AB1F
.故當(dāng)點(diǎn)F是CD的中點(diǎn)時(shí),D1E⊥平面AB1F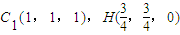 ,
,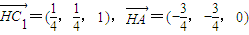 .
.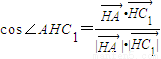 ,
,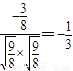 ,
,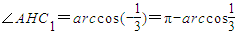 .
. .
.


| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,在棱長都相等的正三棱柱ABC-A1B1C1中,D,E分別為AA1,B1C的中點(diǎn).
如圖,在棱長都相等的正三棱柱ABC-A1B1C1中,D,E分別為AA1,B1C的中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
 如圖,在棱長都相等的正三棱柱ABC-A1B1C1中,D,E分別為AA1,B1C的中點(diǎn).
如圖,在棱長都相等的正三棱柱ABC-A1B1C1中,D,E分別為AA1,B1C的中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2009-2010學(xué)年江蘇省南京市金陵中學(xué)高三(上)8月月考數(shù)學(xué)試卷(解析版) 題型:解答題

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012年安徽省合肥八中高考數(shù)學(xué)一模試卷(理科)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com