
【題目】O為坐標原點,直線l與圓x2+y2=2相切.
(1)若直線l分別與x、y軸正半軸交于A、B兩點,求△AOB面積的最小值及面積取得最小值時的直線l的方程.
(2)設直線l交橢圓 ![]() =1于P、Q兩點,M為PQ的中點,求|OM|的取值范圍.
=1于P、Q兩點,M為PQ的中點,求|OM|的取值范圍.
【答案】
(1)解:設直線l的方程為 ![]() =1(a,b>0),
=1(a,b>0),
由直線和圓x2+y2=4相切,可得 ![]() =
= ![]() ,
,
即有 ![]() =
= ![]() ≥
≥ ![]() ,即ab≥4,
,即ab≥4,
當且僅當a=b=2時,取得等號.
則△AOB面積S= ![]() ab的最小值為2;
ab的最小值為2;
此時直線的方程為x+y﹣2=0
(2)解:若直線的斜率不存在,設為x=t,
由直線和圓相切可得,t=﹣ ![]() 或
或 ![]() .
.
代入橢圓方程可得,y=± ![]() ,
,
可得中點M坐標為(﹣ ![]() ,0)或(
,0)或( ![]() ,0),|OM|=
,0),|OM|= ![]() ;
;
設直線l的方程為y=kx+m,代入橢圓方程可得,
(1+2k2)x2+4kmx+2m2﹣6=0,
△=16k2m2﹣4(1+2k2)(2m2﹣6)>0,
即為m2<3+6k2,
由直線和圓相切,可得 ![]() =
= ![]() ,
,
即為m2=2+2k2,由2+2k2<3+6k2,可得k∈R,
設P,Q的坐標為(x1,y1),(x2,y2),
可得x1+x2=﹣ ![]() ,中點M的坐標為(﹣
,中點M的坐標為(﹣ ![]() ,
, ![]() ),
),
即有|OM|= ![]() =
= ![]()
設1+2k2=t(t≥1),則|OM|= ![]() =
= ![]()
= ![]() ,由t≥1可得t=2取得最大值
,由t≥1可得t=2取得最大值 ![]() ,
,
t=1時,取得最小值 ![]() .
.
故|OM|的范圍是[ ![]() ,
, ![]() ]
]
【解析】(1)設出直線方程,由直線和圓相切的條件:d=r,結合基本不等式,即可得到面積的最小值和此時直線的方程;(2)討論直線的斜率不存在和存在,設出直線方程為y=kx+m,代入橢圓方程,運用韋達定理和中點坐標公式,結合判別式大于0,化簡整理即可得到所求范圍.


科目:高中數學 來源: 題型:
【題目】如圖,在矩形![]() 中
中![]() ,E為
,E為![]() 的中點,將
的中點,將![]() 沿
沿![]() 翻折到
翻折到![]() 的位置,
的位置,![]() 平面
平面![]() ,
,![]() 為
為![]() 的中點,則在翻折過程中,下列結論正確的是( )
的中點,則在翻折過程中,下列結論正確的是( )
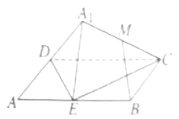
A.恒有![]() 平面
平面![]()
B.B與M兩點間距離恒為定值
C.三棱錐![]() 的體積的最大值為
的體積的最大值為![]()
D.存在某個位置,使得平面![]() ⊥平面
⊥平面![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
已知![]() 是遞增數列,其前
是遞增數列,其前![]() 項和為
項和為![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求數列![]() 的通項
的通項![]() ;
;
(Ⅱ)是否存在![]() 使得
使得![]() 成立?若存在,寫出一組符合條件的
成立?若存在,寫出一組符合條件的![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(Ⅲ)設![]() ,若對于任意的
,若對于任意的![]() ,不等式
,不等式
![]() 恒成立,求正整數
恒成立,求正整數![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司開設的某險種的基本保費為![]() 萬元,今年參加該保險的人來年繼續購買該險種的投保人稱為續保人,續保人的下一年度的保費與其與本年度的出險次數的關聯如下:
萬元,今年參加該保險的人來年繼續購買該險種的投保人稱為續保人,續保人的下一年度的保費與其與本年度的出險次數的關聯如下:
本年度出險次數 |
|
|
|
|
|
|
下一次保費(單位:萬元) |
|
|
|
|
|
|
設今年初次參保該險種的某人準備來年繼續參保該險種,且該參保人一年內出險次數的概率分布列如下:
一年內出險次數 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
(![]() )求此續保人來年的保費高于基本保費的概率.
)求此續保人來年的保費高于基本保費的概率.
(![]() )若現如此續保人來年的保費高于基本保費,求其保費比基本保費高出
)若現如此續保人來年的保費高于基本保費,求其保費比基本保費高出![]() 的概率.
的概率.
(![]() )求該續保人來年的平均保費與基本保費的比值.
)求該續保人來年的平均保費與基本保費的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我市物價監督部門為調研某公司新開發上市的一種產品銷售價格的合理性,對該公司的產品的銷售與價格進行了統計分析,得到如下數據和散點圖:
定價 | 10 | 20 | 30 | 40 | 50 | 60 |
年銷售 | 1150 | 643 | 424 | 262 | 165 | 86 |
| 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

圖(1)為![]() 散點圖,圖(2)為
散點圖,圖(2)為![]() 散點圖.
散點圖.
(Ⅰ)根據散點圖判斷![]() 與
與![]() ,
,![]() 與
與![]() 哪一對具有較強的線性相關性(不必證明);
哪一對具有較強的線性相關性(不必證明);
(Ⅱ)根據(Ⅰ)的判斷結果和參考數據,建立![]() 關于
關于![]() 的回歸方程(線性回歸方程中的斜率和截距均保留兩位有效數字);
的回歸方程(線性回歸方程中的斜率和截距均保留兩位有效數字);
(Ⅲ)定價為多少時,年銷售額的預報值最大?(注:年銷售額![]() 定價
定價![]() 年銷售)
年銷售)
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
參考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4﹣4:極坐標與參數方程
極坐標系與直角坐標系xOy有相同的長度單位,以原點O為極點,以x軸正半軸為極軸.已知曲線C1的極坐標方程為 ![]() ,曲線C2的極坐標方程為ρsinθ=a(a>0),射線
,曲線C2的極坐標方程為ρsinθ=a(a>0),射線 ![]() ,
, ![]() 與曲線C1分別交異于極點O的四點A,B,C,D.
與曲線C1分別交異于極點O的四點A,B,C,D.
(Ⅰ)若曲線C1關于曲線C2對稱,求a的值,并把曲線C1和C2化成直角坐標方程;
(Ⅱ)求|OA||OC|+|OB||OD|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,
,![]() 是橢圓上一點.
是橢圓上一點.
(1)求橢圓的標準方程;
(2)過橢圓右焦點![]() 的直線與橢圓交于
的直線與橢圓交于![]() 兩點,
兩點,![]() 是直線
是直線![]() 上任意一點.證明:直線
上任意一點.證明:直線![]() 的斜率成等差數列.
的斜率成等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB是圓O的直徑,C為圓周上一點,過C作圓O的切線l,過A作直線l的垂線AD,D為垂足,AD與圓O交于點E. 
(1)求證:ABDE=BCCE;
(2)若AB=8,BC=4,求線段AE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com