【題目】已知f（x）=x3+3x2+a（a為常數），在[﹣3，3]上有最小值3，那么在[﹣3，3]上f（x）的最大值是 ．
【答案】57
【解析】解析：f′（x）=3x2+6x，令f′（x）=0，得3x（x+2）=0x=0，x=﹣2．
（i）當0≤x≤3，或﹣3≤x≤﹣2時，f′（x）≥0，f（x）單調遞增，
（ii）當﹣2＜x＜0時，f（x）單調遞減，由最小值為3知，最小為f（﹣3）或f（0）
f（﹣3）=（﹣3）3+3×（﹣3）2+a=a，f（0）=a，則a=3，
∴f（x）=x3+3x2+3，其最大值為f（﹣2）或f（3），
f（﹣2）=（﹣2）3+3×（﹣2）2+3=7，f（3）=33+3×32+3=57，則最大值為57．
所以答案是：57．
【考點精析】認真審題，首先需要了解函數的最大(小)值與導數(求函數
在
上的最大值與最小值的步驟：（1）求函數在
內的極值；（2）將函數的各極值與端點處的函數值
，
比較，其中最大的是一個最大值，最小的是最小值)．
口算題卡加應用題集訓系列答案
綜合自測系列答案科目：高中數學 來源： 題型：
【題目】在四棱錐P﹣ABCD中，底面ABCD是邊長為2的菱形，∠BAD=60°，PD⊥底面ABCD，點M、N分別是棱AB、CD的中點．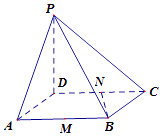 
（1）證明：BN⊥平面PCD；
（2）在線段PC上是否存在點H，使得MH與平面PCD所成最大角的正切值為 
，若存在，請求出H點的位置；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=（x2+ax+a）e﹣x ， （a為常數，e為自然對數的底）．
（1）當a=0時，求f′（2）；
（2）若f（x）在x=0時取得極小值，試確定a的取值范圍；
（3）在（2）的條件下，設由f（x）的極大值構成的函數為g（a），將a換元為x，試判斷曲線y=g（x）是否能與直線3x﹣2y+m=0（m為確定的常數）相切，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】記所有非零向量構成的集合為V，對于 
， 
∈V， ≠ ，定義V（ ， ）=|x∈V|x =x |
（1）請你任意寫出兩個平面向量 ， ，并寫出集合V（ ， ）中的三個元素；
（2）請根據你在（1）中寫出的三個元素，猜想集合V（ ， ）中元素的關系，并試著給出證明；
（3）若V（ ， ）=V（ ， 
），其中 ≠ ，求證：一定存在實數λ1 ， λ2 ， 且λ1+λ2=1，使得 =λ1 +λ2 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種產品的廣告費支出x與銷售額y（單位：百萬元）之間有如下對應數據：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 50 | 60 | 70 |
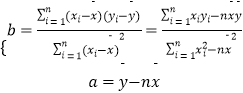
（1）畫出散點圖；
（2）求線性回歸方程；
（3）預測當廣告費支出為7百萬元時的銷售額．參考公式：．
查看答案和解析>>
科目：高中數學 來源： 題型：
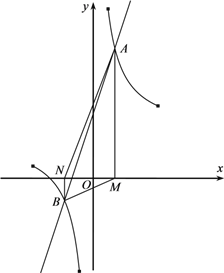
【題目】如圖，已知直線
與曲線
在第一象限和第三象限分別交于點
和點
，分別由點
、
向
軸作垂線，垂足分別為
、
，記四邊形
的面積為S.
⑴ 求出點
、
的坐標及實數
的取值范圍；
⑵ 當
取何值時，S取得最小值，并求出S的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）=sin2x+2 
cos2x﹣ ，函數g（x）=mcos（2x﹣ 
）﹣2m+3（m＞0），若存在x1 ， x2∈[0， 
]，使得f（x1）=g（x2）成立，則實數m的取值范圍是（ ）
A.（0，1]
B.[1，2]
C.[ 
，2]
D.[ ， 
]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
