
【題目】已知三次函數f(x)=x3+bx2+cx+d(a,b,c∈R)過點(3,0),且函數f(x)在點(0,f(0))處的切線恰好是直線y=0.
(1)求函數f(x)的解析式;
(2)設函數g(x)=9x+m﹣1,若函數y=f(x)﹣g(x)在區間[﹣2,1]上有兩個零點,求實數m的取值范圍.
【答案】
(1)解:f′(x)=3x2+2bx+c,由已知條件得:
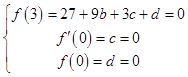 ,解得b=﹣3,c=d=0;
,解得b=﹣3,c=d=0;
∴f(x)=x3﹣3x2
(2)解:由已知條件得:f(x)﹣g(x)=0在[﹣2,1]上有兩個不同的解;
即x3﹣3x2﹣9x﹣m+1=0在區間[﹣2,1]有兩個不同的解;
即m=x3﹣3x2﹣9x+1在[﹣2,1]上有兩個不同解.
令h(x)=x3﹣3x2﹣9x+1,h′(x)=3x2﹣6x﹣9,x∈[﹣2,1];
解3x2﹣6x﹣9>0得:﹣2≤x<﹣1;解3x2﹣6x﹣9<0得:﹣1<x≤1;
∴h(x)max=h(﹣1)=6,又f(﹣2)=﹣1,f(1)=﹣10,∴h(x)min=﹣10;
m=h(x)在區間[﹣2,1]上有兩個不同的解,∴﹣1≤m<6.
∴實數m的取值范圍是[﹣1,6)
【解析】(1)根據已知條件即可建立關于b,c,d的三個方程,解方程即可求出b,c,d,從而求出f(x)的解析式.(2)由已知條件可得到方程f(x)﹣g(x)=0在區間[﹣2,1]上有兩個不同的解,帶入f(x),g(x)后得到:方程x3﹣3x2﹣9x﹣m+1=0在區間[﹣2,1]上有兩個不同解.因為求m的取值范圍,所以把方程變成:m=x3﹣3x2﹣9x+1,求函數x3﹣3x2﹣9x+1在區間[﹣2,1]上的取值范圍,要使方程有兩個不同的解,從而求出m應滿足的范圍.這樣便求出了m的取值范圍.
【考點精析】解答此題的關鍵在于理解函數的最大(小)值與導數的相關知識,掌握求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:
【題目】在一次耐力和體能測試之后,某校對其甲、乙、丙、丁四位學生的耐力成績(![]() )和體能成績(
)和體能成績(![]() )進行回歸分析,求得回歸直線方程為
)進行回歸分析,求得回歸直線方程為![]() .由于某種原因,成績表(如下表所示)中缺失了乙的耐力和體能成績.
.由于某種原因,成績表(如下表所示)中缺失了乙的耐力和體能成績.
甲 | 乙 | 丙 | 丁 | |
耐力成績(X) | 7.5 | m | 8 | 8.5 |
體能成績(Y) | 8 | n | 8.5 | 9.5 |
綜合素質 ( | 15.5 | 16 | 16.5 | 18 |
(Ⅰ)請設法還原乙的耐力成績![]() 和體能成績
和體能成績![]() ;
;
(Ⅱ)在區域性校際學生身體綜合素質比賽中,由甲、乙、丙、丁四位學生組成學校代表隊參賽.共舉行3場比賽,每場比賽均由賽事主辦方從學校代表中隨機抽兩人參賽,每場比賽所抽的選手中,只要有一名選手的綜合素質分高于16分,就能為所在學校贏得一枚榮譽獎章.若記比賽中贏得榮譽獎章的枚數為![]() ,試根據上表所提供數據,預測該校所獲獎章數
,試根據上表所提供數據,預測該校所獲獎章數![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙、丁四個物體同時從某一點出發向同一個方向運動,其路程fi(x)(i=1,2,3,4)關于時間x(x≥0)的函數關系式分別為f1(x)=2x﹣1,f2(x)=x3 , f3(x)=x,f4(x)=log2(x+1),有以下結論:
①當x>1時,甲走在最前面;
②當x>1時,乙走在最前面;
③當0<x<1時,丁走在最前面,當x>1時,丁走在最前面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它們一直運動下去,最終走在最前面的是甲.
其中,正確結論的序號為(把正確結論的序號都填上,多填或少填均不得分)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】曲線![]() 是平面內與兩個定點
是平面內與兩個定點![]() ,
, ![]() 的距離之積等于
的距離之積等于![]() 的點的軌跡.給出下列命題:
的點的軌跡.給出下列命題:
①曲線![]() 過坐標原點;
過坐標原點;
②曲線![]() 關于坐標軸對稱;
關于坐標軸對稱;
③若點![]() 在曲線
在曲線![]() 上,則
上,則![]() 的周長有最小值
的周長有最小值![]() ;
;
④若點![]() 在曲線
在曲線![]() 上,則
上,則![]() 面積有最大值
面積有最大值![]() .
.
其中正確命題的個數為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖表示某人的體重與年齡的關系,則( )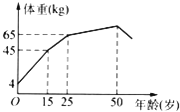
A.體重隨年齡的增長而增加
B.25歲之后體重不變
C.體重增加最快的是15歲至25歲
D.體重增加最快的是15歲之前
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() .
.
(1)當a>0時,求函數f(x)的單調區間;
(2)若f(x)在[1,e]上的最小值為1,求實數a的取值范圍;(其中e為自然對數的底數);
(3)若 ![]() 上恒成立,求實數a的取值范圍.
上恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓C1: ![]() +y2=1,雙曲線C2:
+y2=1,雙曲線C2: ![]() =1(a>0,b>0),若以C1的長軸為直徑的圓與C2的一條漸近線交于A,B兩點,且C1與該漸近線的兩交點將線段AB三等分,則C2的離心率為( )
=1(a>0,b>0),若以C1的長軸為直徑的圓與C2的一條漸近線交于A,B兩點,且C1與該漸近線的兩交點將線段AB三等分,則C2的離心率為( ) 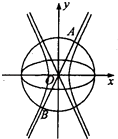
A.![]()
B.5
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有甲、乙、丙、丁4個學生課余參加學校社團文學社與街舞社的活動,每人參加且只能參加一個社團的活動,且參加每個社團是等可能的.
(1)求文學社和街舞社都至少有1人參加的概率;
(2)求甲、乙同在一個社團,且丙、丁不同在一個社團的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com