
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),在以坐標原點為極點,
為參數),在以坐標原點為極點,![]() 軸的正半軸為極軸的極坐標系中,直線
軸的正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若直線![]() 與曲線
與曲線![]() 至多只有一個公共點,求實數
至多只有一個公共點,求實數![]() 的取值范圍;
的取值范圍;
(2)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,且
兩點,且![]() ,
,![]() 的中點為
的中點為![]() ,求點
,求點![]() 的軌跡方程.
的軌跡方程.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】
(1)利用參數方程、極坐標方程與直角坐標方程的互化公式把曲線![]() 和直線
和直線![]() 的方程化為直角坐標方程,并聯立直線
的方程化為直角坐標方程,并聯立直線![]() 和曲線
和曲線![]() 的直角坐標方程,得到關于
的直角坐標方程,得到關于![]() 的一元二次方程,利用判別式
的一元二次方程,利用判別式![]() 即可求出實數
即可求出實數![]() 的取值范圍;
的取值范圍;
![]() 根據題意,設
根據題意,設![]() ,
,![]() ,
,![]() 的中點
的中點![]() 為
為![]() ,直線
,直線![]() 和曲線
和曲線![]() 的直角坐標方程聯立,得到關于
的直角坐標方程聯立,得到關于![]() 的一元二次方程,由兩個交點
的一元二次方程,由兩個交點![]() ,
,![]() 可得判別式
可得判別式![]() ,求出
,求出![]() 取值范圍,利用韋達定理和點
取值范圍,利用韋達定理和點![]() 在直線
在直線![]() 上表示出點
上表示出點![]() 坐標,消去參數
坐標,消去參數![]() 即可求出
即可求出![]() ,
,![]() 的中點
的中點![]() 的軌跡方程.
的軌跡方程.
(1)因為曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),
為參數),
消去參數![]() 可得,曲線
可得,曲線![]() 的直角坐標方程為
的直角坐標方程為![]() ,
,
由題意知,直線![]() 的極坐標方程可化為
的極坐標方程可化為![]() ,
,
因為![]() ,所以直線
,所以直線![]() 的直角坐標方程為
的直角坐標方程為![]() ,
,
聯立方程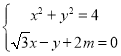 ,可得
,可得![]() ,
,
因為直線![]() 與曲線
與曲線![]() 至多只有一個公共點,
至多只有一個公共點,
所以判別式![]() ,解得
,解得![]() 或
或![]() ,
,
所以所求實數![]() 的取值范圍為
的取值范圍為![]() 或
或![]() .
.
(2)設![]() ,
,![]() ,
,![]() 的中點
的中點![]() 為
為![]() ,
,
聯立方程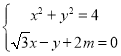 ,可得
,可得![]() ,
,
所以判別式![]() ,解得
,解得![]() ,
,
由韋達定理可得,![]() ,
,
因為點![]() 在直線
在直線![]() 上,所以
上,所以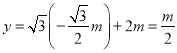 ,
,
所以可得![]() ,
,![]() 即為點
即為點![]() 的軌跡方程.
的軌跡方程.


 快捷英語周周練系列答案
快捷英語周周練系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓G:![]() 的右焦點為F,過F的直線l交橢圓于A、B兩點,直線與l不與坐標軸平行,若AB的中點為N,O為坐標原點,直線ON交直線x=3于點M.
的右焦點為F,過F的直線l交橢圓于A、B兩點,直線與l不與坐標軸平行,若AB的中點為N,O為坐標原點,直線ON交直線x=3于點M.
(1)求證:MF⊥l;
(2)求![]() 的最大值,
的最大值,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 的兩個頂點
的兩個頂點![]() 的坐標分別為
的坐標分別為![]() ,
,![]() ,且
,且![]() 所在直線的斜率之積等于
所在直線的斜率之積等于![]() ,記頂點
,記頂點![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求頂點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,點
兩點,點![]() 在曲線
在曲線![]() 上,且
上,且![]() 為
為![]() 的重心(
的重心(![]() 為坐標原點),求證:
為坐標原點),求證:![]() 的面積為定值,并求出該定值.
的面積為定值,并求出該定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為等差數列,
為等差數列,![]() 為等比數列,公比為
為等比數列,公比為![]() .令
.令![]() .
.
(1)若![]() .
.
①當![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
②設![]() ,
,![]() ,試比較
,試比較![]() 與
與![]() 的大小?并證明你的結論.
的大小?并證明你的結論.
(2)問集合![]() 中最多有多少個元素?并證明你的結論.
中最多有多少個元素?并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第18屆國際籃聯籃球世界杯(世界男子籃球錦標賽更名為籃球世界杯后的第二屆世界杯)于2019年8月31日至9月15日在中國的北京、廣州、南京、上海、武漢、深圳、佛山、東莞八座城市舉行.中國隊12名球員在第一場和第二場得分的莖葉圖如圖所示,則下列說法正確的是( )

A.第一場得分的中位數為![]() B.第二場得分的平均數為
B.第二場得分的平均數為![]()
C.第一場得分的極差大于第二場得分的極差D.第一場與第二場得分的眾數相等
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在邊長為3的正方形ABCD中,點E,F分別在邊AB,BC上(如圖1),且BE=BF,將△AED,△DCF分別沿DE,DF折起,使A,C兩點重合于點A′(如圖2).

(1)求證:A′D⊥EF;
(2)BF![]() BC時,求點A′到平面DEF的距離.
BC時,求點A′到平面DEF的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 為
為![]() 的中點,點
的中點,點![]() 為線段
為線段![]() 垂直平分線上的一點,且
垂直平分線上的一點,且![]() ,固定邊
,固定邊![]() ,在平面
,在平面![]() 內移動頂點
內移動頂點![]() ,使得
,使得![]() 的內切圓始終與
的內切圓始終與![]() 切于線段
切于線段![]() 的中點,且
的中點,且![]() 、
、![]() 在直線
在直線![]() 的同側,在移動過程中,當
的同側,在移動過程中,當![]() 取得最小值時,
取得最小值時,![]() 的面積為( )
的面積為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一島礁旁有兩條航道![]() 與
與![]() ,
,![]() .一日,我方船只甲在
.一日,我方船只甲在![]() 航道上巡邏,在與
航道上巡邏,在與![]() 相距50公里的點
相距50公里的點![]() 處,發現不明身份的船乙剛駛過點
處,發現不明身份的船乙剛駛過點![]() ,并沿
,并沿![]() 方向以40公里/小時的速度運動,船甲立即沿
方向以40公里/小時的速度運動,船甲立即沿![]() 方向以
方向以![]() 公里/小時(
公里/小時(![]() )的速度追擊,且甲到達點
)的速度追擊,且甲到達點![]() 即停止前行(乙可繼續前進).設甲出發時,經過
即停止前行(乙可繼續前進).設甲出發時,經過![]() 小時甲,乙之間的距離為
小時甲,乙之間的距離為![]() 公里,當
公里,當![]() 最小時,可以達到最佳的驅離距離.
最小時,可以達到最佳的驅離距離.
(1)試求![]() 的解析式,并寫出定義域;
的解析式,并寫出定義域;
(2)求最多經過多長時間,我船可以達到最佳的驅離距離?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:若函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ,則稱區間
,則稱區間![]() 是函數
是函數![]() 的“完美區間”,另外,定義區間
的“完美區間”,另外,定義區間![]() 的“復區間長度”為
的“復區間長度”為![]() ,已知函數
,已知函數![]() ,則( )
,則( )
A.![]() 是
是![]() 的一個“完美區間”
的一個“完美區間”
B. 是
是![]() 的一個“完美區間”
的一個“完美區間”
C.![]() 的所有“完美區間”的“復區間長度”的和為
的所有“完美區間”的“復區間長度”的和為![]()
D.![]() 的所有“完美區間”的“復區間長度”的和為
的所有“完美區間”的“復區間長度”的和為![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com