Question

已知數列{a_n}是等比數列，其首項a₁=1，公比為2；數列{b_n}是等差數列，其首項b₁=1，公差為d，且其前n項的和S_n滿足S₇=14S₂；
（I）求數列{a_n+b_n}的前n項的和T_n；
（II）在數列{a_n}（n=1，2，3，4）中任取一項a_i，在數列{b_n}（1，2，3，4）中任取一項b_k，試求滿足a_i²+b_i²≤81的概率．

Answer 1

【答案】分析：（I）由題意得a_n=2^n-1，b_n=1+（n-1）d，由S₇=14S₂，得d=3，由此能求出數列{a_n+b_n}的前n項的和T_n；
（II）a_i=2^i-1，i為1，2，4，8；b_k=3k-2，i為1，4，7，10．有序實數對（a_i，b_k）共有16個，分類討論知滿足題意的點共11個，由此能求出滿足a_i²+b_i²≤81的概率．
解答：解：（I）由題意得：a_n=2^n-1，b_n=1+（n-1）d，由S₇=14S₂，得d=3
∴
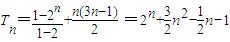
（II）a_i=2^i-1，i為1，2，4，8；b_k=3k-2，i為1，4，7，10
有序實數對（a_i，b_k）共有16個，
當a₁=1時，b_k取1，4，7共3個；當a₂=2時，b_k取1，4，7共3個
當a₃=4時，b_k取1，4，7共3個；當a₄=8時，b_k取1，4共2個；
滿足題意的點共11個，所求的概率為．
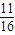
點評：本題考查數列的性質和應用，解題時要注意公式的靈活運用．
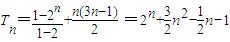
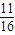