
 =(l,m,n)是平面ABD的法向量,由(Ⅰ)易得向量
=(l,m,n)是平面ABD的法向量,由(Ⅰ)易得向量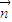 的坐標,同時易得
的坐標,同時易得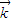 =(0,0,1)是平面ABC的法向量,由向量的夾角公式可得從而cos<
=(0,0,1)是平面ABC的法向量,由向量的夾角公式可得從而cos<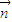 ,
,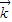 >,進而由同角三角函數(shù)的基本關(guān)系,可得tan<
>,進而由同角三角函數(shù)的基本關(guān)系,可得tan<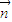 ,
,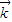 >,即可得答案.
>,即可得答案.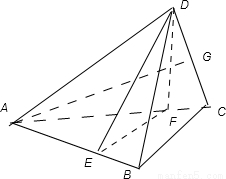 解:法一
解:法一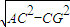 =
=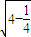 =
=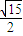 ;
; AC•DF=
AC•DF= CD•AG可得,DF=
CD•AG可得,DF=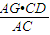 =
=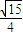 ;
;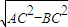 =
=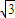 ,
, AB•BC=
AB•BC=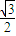 ;
; ×S△ABC×DF=
×S△ABC×DF=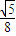 ;
;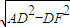 =
=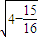 =
= ;
;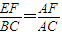 ,可得EF=
,可得EF= ;
; =
=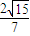 .
.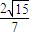 .
.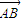 ⊥
⊥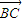 ,|
,|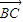 |=1;
|=1;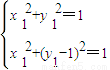 ,
,
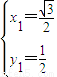 或
或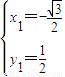 (舍);
(舍);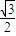 ,
, ,0),
,0),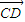 |=1,|
|=1,|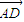 |=2,有(y2-1)2+z22=1且(y2+1)2+z22=1;
|=2,有(y2-1)2+z22=1且(y2+1)2+z22=1; 或
或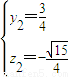 (舍),
(舍), ,
,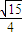 ),
),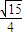
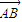 |=
|=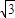 ,|
,|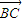 |=1;
|=1; ×
× ×|
×|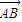 |×|
|×|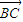 |h=
|h=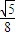 ;
;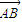 =(
=(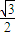 ,
, ,0),
,0),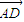 =(0,
=(0, ,
,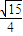 ),
),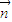 =(l,m,n)是平面ABD的法向量,則由
=(l,m,n)是平面ABD的法向量,則由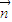 ⊥
⊥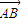 可得,
可得,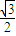 l+
l+ m=0,(1);
m=0,(1);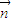 ⊥
⊥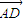 可得,
可得, m+
m+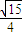 n=0,(2);
n=0,(2);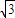 ,n=
,n=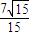 ,即
,即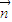 =(
=(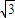 ,-1,
,-1,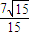 )
)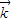 =(0,0,1)是平面ABC的法向量,
=(0,0,1)是平面ABC的法向量, ,
,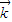 >=
>=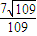 ;
;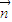 ,
, >=
>=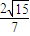 ;
; .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:
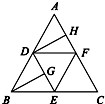 如圖,在正三角形ABC中,D,E,F(xiàn)分別為各邊的中點,G,H分別為DE,AF的中點,將△ABC沿DE,EF,DF折成正四面體P-DEF,則四面體中異面直線PG與DH所成的角的余弦值為
如圖,在正三角形ABC中,D,E,F(xiàn)分別為各邊的中點,G,H分別為DE,AF的中點,將△ABC沿DE,EF,DF折成正四面體P-DEF,則四面體中異面直線PG與DH所成的角的余弦值為查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
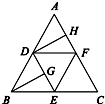 如圖,在正三角形ABC中,D,E,F(xiàn)分別為各邊的中點,G,H分別為DE,AF的中點,將△ABC沿DE,EF,DF折成正四面體P-DEF,則四面體中異面直線PG與DH所成的角的余弦值為( )
如圖,在正三角形ABC中,D,E,F(xiàn)分別為各邊的中點,G,H分別為DE,AF的中點,將△ABC沿DE,EF,DF折成正四面體P-DEF,則四面體中異面直線PG與DH所成的角的余弦值為( )
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
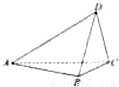
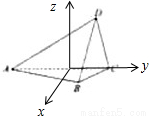
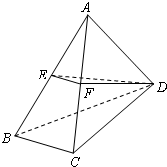 如圖,在四面體ABCD中,BC⊥面ACD,DA=DC,E、F分別為AB、AC的中點.
如圖,在四面體ABCD中,BC⊥面ACD,DA=DC,E、F分別為AB、AC的中點.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
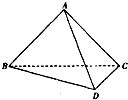 (2009•武漢模擬)如圖,在四面體A-BCD中,AB=AD=
(2009•武漢模擬)如圖,在四面體A-BCD中,AB=AD=| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
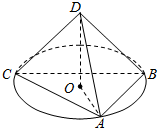 如圖,在四面體ABCD中,DA=DB=DC=1,且DA,DB,DC兩兩互相垂直,點O是△ABC的中心,將△DAO繞直線DO旋轉(zhuǎn)一周,則在旋轉(zhuǎn)過程中,直線DA與BC所成角的余弦值的取值范圍是( )
如圖,在四面體ABCD中,DA=DB=DC=1,且DA,DB,DC兩兩互相垂直,點O是△ABC的中心,將△DAO繞直線DO旋轉(zhuǎn)一周,則在旋轉(zhuǎn)過程中,直線DA與BC所成角的余弦值的取值范圍是( )A、[0,
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、[0,
|
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com