
【題目】已知函數f(x)=2lnx﹣x.
(I)寫出函數f(x)的定義域,并求其單調區間;
(II)已知曲線y=f(x)在點(x0,f(x0))處的切線為l,且l在y軸上的截距是﹣2,求x0.
【答案】(Ⅰ)定義域為(0,+∞), 單調遞增區間是(0,2),單調遞減區間是(2,+∞);(Ⅱ)1.
【解析】
(Ⅰ)由對數真數大于零求得函數的定義域,利用導數求得函數的單調區間.(Ⅱ)利用切點的橫坐標求得斜率,由點斜式寫出切線方程,令縱截距為![]() 列方程,解方程求得
列方程,解方程求得![]() 的值.
的值.
解:(Ⅰ)函數y=f(x)的定義域為:(0,+∞).
∵f(x)=2lnx﹣x,∴![]() .
.
令f'(x)=0,則x=2.
當x在(0,+∞)上變化時,f'(x),f(x)的變化情況如下表
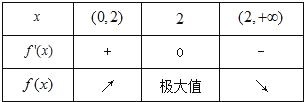
∴函數y=f(x)的單調遞增區間是(0,2),單調遞減區間是(2,+∞).
(Ⅱ)由題意可知:f(x0)=2lnx0﹣x0,
曲線y=f(x)在點(x0,f(x0))處的切線的斜率為![]() .
.
∴切線方程為:![]() .
.
∴![]() .
.
∴![]() .
.
∵切線方程為y=kx﹣2,
∴2lnx0﹣2=﹣2.
∴x0=1.


科目:高中數學 來源: 題型:
【題目】![]() 漢字聽寫大會
漢字聽寫大會![]() 不斷創收視新高,為了避免“書寫危機”,弘揚傳統文化,某市大約10萬名市民進行了漢字聽寫測試
不斷創收視新高,為了避免“書寫危機”,弘揚傳統文化,某市大約10萬名市民進行了漢字聽寫測試![]() 現從某社區居民中隨機抽取50名市民的聽寫測試情況,發現被測試市民正確書寫漢字的個數全部在160到184之間,將測試結果按如下方式分成六組:第1組
現從某社區居民中隨機抽取50名市民的聽寫測試情況,發現被測試市民正確書寫漢字的個數全部在160到184之間,將測試結果按如下方式分成六組:第1組![]() ,第2組
,第2組![]() ,
,![]() ,第6組
,第6組![]() ,如圖是按上述分組方法得到的頻率分布直方圖.
,如圖是按上述分組方法得到的頻率分布直方圖.

![]() 若電視臺記者要從抽取的市民中選1人進行采訪,求被采訪人恰好在第2組或第6組的概率;
若電視臺記者要從抽取的市民中選1人進行采訪,求被采訪人恰好在第2組或第6組的概率;
![]() 試估計該市市民正確書寫漢字的個數的平均數與中位數;
試估計該市市民正確書寫漢字的個數的平均數與中位數;
![]() 已知第4組市民中有3名男性,組織方要從第4組中隨機抽取2名市民組成弘揚傳統文化宣傳隊,求至少有1名女性市民的概率.
已知第4組市民中有3名男性,組織方要從第4組中隨機抽取2名市民組成弘揚傳統文化宣傳隊,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雞的產蛋量與雞舍的溫度有關,為了確定下一個時段雞舍的控制溫度,某企業需要了解雞舍的溫度![]() (單位:
(單位:![]() ),對某種雞的時段產蛋量
),對某種雞的時段產蛋量![]() (單位:
(單位:![]() ) 和時段投入成本
) 和時段投入成本![]() (單位:萬元)的影響,為此,該企業收集了7個雞舍的時段控制溫度
(單位:萬元)的影響,為此,該企業收集了7個雞舍的時段控制溫度![]() 和產蛋量
和產蛋量![]() 的數據,對數據初步處理后得到了如圖所示的散點圖和表中的統計量的值.
的數據,對數據初步處理后得到了如圖所示的散點圖和表中的統計量的值.
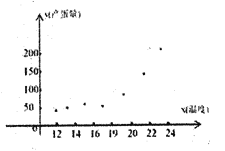
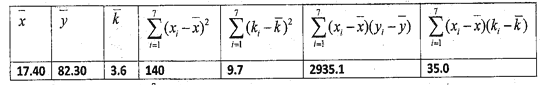
其中![]() .
.
(1)根據散點圖判斷,![]() 與
與![]() 哪一個更適宜作為該種雞的時段產蛋量
哪一個更適宜作為該種雞的時段產蛋量![]() 關于雞舍時段控制溫度
關于雞舍時段控制溫度![]() 的回歸方程類型?(給判斷即可,不必說明理由)
的回歸方程類型?(給判斷即可,不必說明理由)
(2)若用![]() 作為回歸方程模型,根據表中數據,建立
作為回歸方程模型,根據表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)已知時段投入成本![]() 與
與![]() 的關系為
的關系為![]() ,當時段控制溫度為
,當時段控制溫度為![]() 時,雞的時段產蛋量及時段投入成本的預報值分別是多少?
時,雞的時段產蛋量及時段投入成本的預報值分別是多少?
附:①對于一組具有線性相關關系的數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為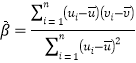 ,
,![]() .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P(2,0),且圓C:x2+y2﹣6x+4y+4=0.
(Ⅰ)當直線![]() 過點P且與圓心C的距離為1時,求直線
過點P且與圓心C的距離為1時,求直線![]() 的方程;
的方程;
(Ⅱ)設過點P的直線與圓C交于A、B兩點,若|AB|=4,求以線段AB為直徑的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司準備將![]() 萬元資金投入到市環保工程建設中,現有甲、乙兩個建設項目選擇,若投資甲項目一年后可獲得的利潤
萬元資金投入到市環保工程建設中,現有甲、乙兩個建設項目選擇,若投資甲項目一年后可獲得的利潤![]() (萬元)的概率分布列如表所示:
(萬元)的概率分布列如表所示:
|
|
|
|
|
|
|
|
且![]() 的期望
的期望![]() ;若投資乙項目一年后可獲得的利潤
;若投資乙項目一年后可獲得的利潤![]() (萬元)與該項目建設材料的成本有關,在生產的過程中,公司將根據成本情況決定是否在第二和第三季度進行產品的價格調整,兩次調整相互獨立且調整的概率分別為
(萬元)與該項目建設材料的成本有關,在生產的過程中,公司將根據成本情況決定是否在第二和第三季度進行產品的價格調整,兩次調整相互獨立且調整的概率分別為![]() 和
和![]() .若乙項目產品價格一年內調整的次數
.若乙項目產品價格一年內調整的次數![]() (次數)與
(次數)與![]() 的關系如表所示:
的關系如表所示:
|
|
|
|
|
|
|
|
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的分布列;
的分布列;
(Ⅲ)若該公司投資乙項目一年后能獲得較多的利潤,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】合肥一中、六中為了加強交流,增進友誼,兩校準備舉行一場足球賽,由合肥一中版畫社的同學設計一幅矩形宣傳畫,要求畫面面積為![]() ,畫面的上、下各留
,畫面的上、下各留![]() 空白,左、右各留
空白,左、右各留![]() 空白.
空白.

(1)如何設計畫面的高與寬的尺寸,才能使宣傳畫所用紙張面積最小?
(2)設畫面的高與寬的比為![]() ,且
,且![]() ,求
,求![]() 為何值時,宣傳畫所用紙張面積最小?
為何值時,宣傳畫所用紙張面積最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】劉徽是我國魏晉時期著名的數學家,他編著的《海島算經》中有一問題:“今有望海島,立兩表齊,高三丈,前后相去千步,令后表與前表相直。從前表卻行一百二十三步,人目著地取望島峰,與表末參合。從后表卻行百二十七步,人目著地取望島峰,亦與表末參合。問島高幾何?” 意思是:為了測量海島高度,立了兩根表,高均為5步,前后相距1000步,令后表與前表在同一直線上,從前表退行123步,人恰觀測到島峰,從后表退行127步,也恰觀測到島峰,則島峰的高度為( )(注:3丈=5步,1里=300步)
A. 4里55步 B. 3里125步 C. 7里125步 D. 6里55步
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩地相距![]() 海里,某貨輪勻速行駛從甲地運輸貨物到乙地,運輸成本包括燃料費用和其他費用.已知該貨輪每小時的燃料費與其速度的平方成正比,比例系數為
海里,某貨輪勻速行駛從甲地運輸貨物到乙地,運輸成本包括燃料費用和其他費用.已知該貨輪每小時的燃料費與其速度的平方成正比,比例系數為![]() ,其他費用為每小時
,其他費用為每小時![]() 元,且該貨輪的最大航行速度為
元,且該貨輪的最大航行速度為![]() 海里/小時.
海里/小時.
(![]() )請將該貨輪從甲地到乙地的運輸成本
)請將該貨輪從甲地到乙地的運輸成本![]() 表示為航行速度
表示為航行速度![]() (海里/小時)的函數.
(海里/小時)的函數.
(![]() )要使從甲地到乙地的運輸成本最少,該貨輪應以多大的航行速度行駛?
)要使從甲地到乙地的運輸成本最少,該貨輪應以多大的航行速度行駛?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com