
【題目】某造船公司年造船量是20艘,已知造船![]() 艘的產值函數為
艘的產值函數為![]() (單位:萬元),成本函數為
(單位:萬元),成本函數為![]() (單位:萬元),又在經濟學中,函數
(單位:萬元),又在經濟學中,函數![]() 的邊際函數
的邊際函數![]() 定義為
定義為![]() .
.
(1)求利潤函數![]() 及邊際利潤函數
及邊際利潤函數![]() .(提示:利潤=產值-成本)
.(提示:利潤=產值-成本)
(2)問年造船量安排多少艘時,可使公司造船的年利潤最大?
(3)求邊際利潤函數![]() 的單調遞減區間,并說明單調遞減在本題中的實際意義是什么?
的單調遞減區間,并說明單調遞減在本題中的實際意義是什么?
【答案】(1)![]() 且
且![]() ;(2)12;(3)
;(2)12;(3)![]() 且
且![]() .
.
【解析】
(1)先根據利潤=產值-成本求P(x),再求邊際利潤函數![]() .(2)利用導數求年造船量安排多少艘時,可使公司造船的年利潤最大.(3)利用二次函數求邊際利潤函數
.(2)利用導數求年造船量安排多少艘時,可使公司造船的年利潤最大.(3)利用二次函數求邊際利潤函數![]() 的單調遞減區間,并說明單調遞減在本題中的實際意義.
的單調遞減區間,并說明單調遞減在本題中的實際意義.
(1)P(x)=R(x)-C(x)=-10x3+45x2+3240x-5(x∈N+,且1≤x≤20);
MP(x)=P(x+1)-P(x)=-30x2+60x+3275(x∈N+,且1≤x≤19).
(2)P'(x)=-30x2+90x+3240=-30(x-12)(x+9),
∵x>0,∴P'(x)=0時,x=12,
∴當0<x<12時,P'(x)>0,
當x>12時,P'(x)<0,∴x=12時,P(x)有最大值.
即年造船量安排12艘時,可使公司造船的年利潤最大.
(3)MP(x)=-30x2+60x+3275=-30(x-1)2+3305.所以,當x≥1時,MP(x)是減函數,
所以單調減區間為[1,19],且x∈N+.
MP(x)是減函數的實際意義是:隨著產量的增加,每艘船的利潤與前一艘船的利潤比較,利潤在減少.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() (
(![]() )的上頂點為
)的上頂點為![]() ,圓
,圓![]() 經過點
經過點![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,過點
兩點,過點![]() 作直線
作直線![]() 的垂線
的垂線![]() 交圓
交圓![]() 于另一點
于另一點![]() .若△PQN的面積為3,求直線
.若△PQN的面積為3,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() 是偶函數,求
是偶函數,求![]() 的值;
的值;
(2)設函數![]() ,當
,當![]() 時,
時,![]() 有且只有一個實數根,求
有且只有一個實數根,求![]() 的取值范圍;
的取值范圍;
(3)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有兩個不相等的實數根
上有兩個不相等的實數根![]() ,
,![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在盒子里有大小相同,僅顏色不同的乒乓球共10個,其中紅球5個,白球3個,藍球2個.現從中任取出一球確定顏色后放回盒子里,再取下一個球.重復以上操作,最多取3次,過程中如果取出藍色球則不再取球.
(1)求整個過程中恰好取到2個白球的概率;
(2)求取球次數的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義城為R的函數![]() ,若滿足:①
,若滿足:①![]() ;②當
;②當![]() ,且
,且![]() 時,都有
時,都有![]() ;③當
;③當![]() 且
且![]() 時,都有
時,都有![]() ,則稱
,則稱![]() 為“偏對稱函數”.下列函數是“偏對稱函數”的是( )
為“偏對稱函數”.下列函數是“偏對稱函數”的是( )
A.![]() B.
B.![]()
C.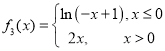 D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】上饒市在某次高三適應性考試中對數學成績數據統計顯示,全市10000名學生的成績近似服從正態分布![]() ,現某校隨機抽取了50名學生的數學成績分析,結果這50名學生的成績全部介于85分到145分之間,現將結果按如下方式分為6組,第一組
,現某校隨機抽取了50名學生的數學成績分析,結果這50名學生的成績全部介于85分到145分之間,現將結果按如下方式分為6組,第一組![]() ,第二組
,第二組![]() ,…,第六組
,…,第六組![]() ,得到如圖所示的頻率分布直方圖:
,得到如圖所示的頻率分布直方圖:
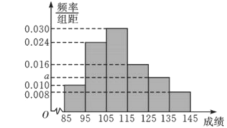
(1)試由樣本頻率分布直方圖估計該校數學成績的平均分數;
(2)若從這50名學生中成績在125分(含125分)以上的同學中任意抽取3人,該3人在全市前13名的人數記為![]() ,求
,求![]() 的概率.
的概率.
附:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com