
【題目】已知數列![]() 的前
的前![]() 項和
項和![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)求數列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1)見解析;(2)![]() .
.
【解析】
試題分析:(1)當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,對
,對![]() 不成立,從而可得數列
不成立,從而可得數列![]() 的通項公式;(2)當
的通項公式;(2)當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]()
![]() ,利用裂項相消法可得
,利用裂項相消法可得![]() ,再驗證
,再驗證![]() 時,是否成立即可.
時,是否成立即可.
試題解析:(1)當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() ,
,
對![]() 不成立,
不成立,
所以數列![]() 的通項公式為
的通項公式為![]() .
.
(2)當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]()
![]()
所以![]()
![]()
又![]() 時,
時,![]() 符合上式,
符合上式,
所以![]() (
(![]() ).
).
【方法點晴】本題主要考查數列的通項公式與求和,以及裂項相消法求數列的和,屬于中檔題. 裂項相消法是最難把握的求和方法之一,其原因是有時很難找到裂項的方向,突破這一難點的方法是根據式子的結構特點,常見的裂項技巧:(1)![]() ;(2)
;(2) ![]()
![]() ; (3)
; (3)![]() ;(4)
;(4)![]()
![]() ;此外,需注意裂項之后相消的過程中容易出現丟項或多項的問題,導致計算結果錯誤.
;此外,需注意裂項之后相消的過程中容易出現丟項或多項的問題,導致計算結果錯誤.


科目:高中數學 來源: 題型:
【題目】在△ABC中,邊a、b、c分別是角A、B、C的對邊,且滿足bcosC=(3a-c)cosB
(1)求cosB
(2)若△ABC的面積為4![]() ,b=4
,b=4![]() ,求△ABC的周長
,求△ABC的周長
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,△ABC為正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中點.求證:

(1)DE=DA;
(2)平面BDM⊥平面ECA;
(3)平面DEA⊥平面ECA.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是首項
是首項![]() 的等差數列,設
的等差數列,設![]() .
.
(1)求證:![]() 是等比數列;
是等比數列;
(2)記![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)在(2)的條件下,記![]() ,若對任意正整數
,若對任意正整數![]() ,不等式
,不等式![]() 恒成立,求整數
恒成立,求整數![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一半徑為2米的水輪如圖所示,水輪圓心![]() 距離水面1米;已知水輪按逆時針做勻速轉動,每3秒轉一圈,如果當水輪上點
距離水面1米;已知水輪按逆時針做勻速轉動,每3秒轉一圈,如果當水輪上點![]() 從水中浮現時(圖中點
從水中浮現時(圖中點![]() )開始計算時間.
)開始計算時間.
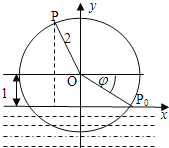
(1)試將點![]() 距離水面的高度
距離水面的高度![]() (單位:米)表示為時間
(單位:米)表示為時間![]() (單位:秒)的函數
(單位:秒)的函數![]() ;
;
(2)點![]() 第一次到達最高點大約要多長時間?
第一次到達最高點大約要多長時間?
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·江蘇高考)如圖,在三棱錐ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,點E,F(E與A,D不重合)分別在棱AD,BD上,且EF⊥AD.

求證:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】伴隨著智能手機的深入普及,支付形式日漸多樣化,打破了傳統支付的局限性和壁壘,有研究表明手機支付的使用比例與人的年齡存在一定的關系,某調研機構隨機抽取了50人,對他們一個月內使用手機支付的情況進行了統計,如下表:

(1)若以“年齡55歲為分界點”,由以上統計數據完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“使用手機支付”與人的年齡有關;
的把握認為“使用手機支付”與人的年齡有關;

(2)若從年齡在![]() ,
,![]() 內的被調查人中各隨機選取2人進行追蹤調查,記選中的4人中“使用手機支付”的人數為
內的被調查人中各隨機選取2人進行追蹤調查,記選中的4人中“使用手機支付”的人數為![]() .
.
①求隨機變量![]() 的分布列;
的分布列;
②求隨機變量![]() 的數學期望.
的數學期望.
參考數據如下:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
參考格式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形,![]() ,
,![]() .
.![]() 是
是![]() 的中點,
的中點,![]() 底面
底面![]() ,
,![]() 在平面
在平面![]() 上的正投影為點
上的正投影為點![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() .
.
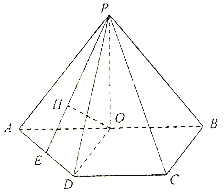
(1)求證:![]() 為
為![]() 中點;
中點;
(2)若![]() ,
,![]() ,在棱
,在棱![]() 上確定一點
上確定一點![]() ,使得
,使得![]() 平面
平面![]() ,并求出
,并求出![]() 與面
與面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的長軸長是短軸長的2倍,且過點
的長軸長是短軸長的2倍,且過點![]() .
.
⑴求橢圓![]() 的方程;
的方程;
⑵若在橢圓上有相異的兩點![]() (
(![]() 三點不共線),
三點不共線),![]() 為坐標原點,且直線
為坐標原點,且直線![]() ,直線
,直線![]() ,直線
,直線![]() 的斜率滿足
的斜率滿足![]() .
.
(ⅰ)求證: ![]() 是定值;
是定值;
(ⅱ)設![]() 的面積為
的面積為![]() ,當
,當![]() 取得最大值時,求直線
取得最大值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com