設m,k為整數,方程mx2-kx+2=0在區間(0,1)內有兩個不同的根,則m+k的最小值為( )
A.-8
B.8
C.12
D.13
【答案】
分析:將一元二次方程的根的分布轉化為確定相應的二次函數的圖象來處理,根據圖象可得到關于m和k的不等式組,此時不妨考慮利用不等式所表示的平面區域來解決,但須注意這不是線性規劃問題,同時注意取整點.
解答:解:設f(x)=mx
2-kx+2,由f(0)=2,易知f(x)的圖象恒過定點(0,2),
因此要使已知方程在區間(0,1)內兩個不同的根,即f(x)的圖象在區間(0,1)內與x軸有兩個不同的交點
即由題意可以得到:必有

,即
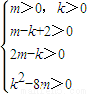
,
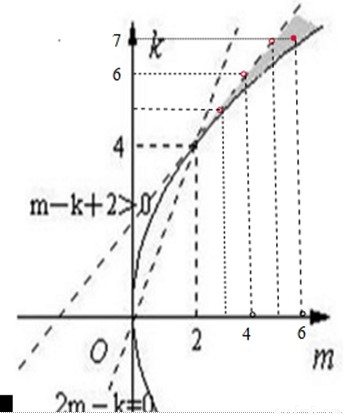
在直角坐標系mok中作出滿足不等式平面區域,
如圖所示,設z=m+k,則直線m+k-z=0經過圖中的陰影中的整點(6,7)時,
z=m+k取得最小值,即z
min=13.
故選D.
點評:此題考查了二次函數與二次方程之間的聯系,解答要注意幾個關鍵點:(1)將一元二次方程根的分布轉化一元二次函數的圖象與x軸的交點來處理;(2)將根據不等式組求兩個變量的最值問題處理為規劃問題;(3)作出不等式表示的平面區域時注意各個不等式表示的公共區域;(4)不可忽視求得最優解是整點.

 ,即
,即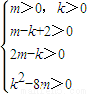 ,
,


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案