(本題滿分14分)
已知函數

且存在

使

(I)證明:

是R上的單調增函數;
(II)設

其中

證明:

(III)證明:

(I)∵
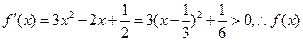
是R上的單調增函數.
(II)∵
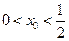
, 即
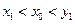
.又

是增函數, ∴
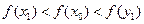
.
即
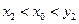
.又
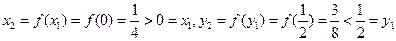
,
綜上,
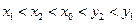
.用數學歸納法證明如下:
(1)當n=1時,上面已證明成立.
(2)假設當n=k(k≥1)時有
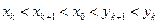
.
當n=k+1時,由

是單調增函數,有
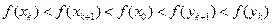
,
∴
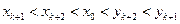
由(1)(2)知對一切n=1,2,…,都有
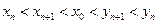
.
(III)
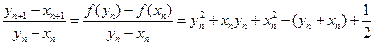
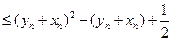
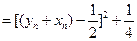
.
由(Ⅱ)知
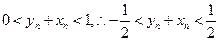
∴
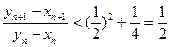
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
設函數
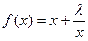
,常數
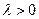
.
(1)若
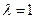
,判斷
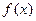
在區間
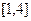
上的單調性,并加以證明;
(2)若
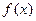
在區間
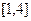
上的單調遞增,求
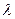
的取值范圍.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知函數
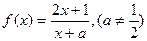
,
(1)若
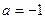
,證明
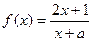
在區間
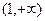
上是增函數;
(2)若
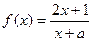
在區間

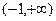
上是單調函數,試求實數
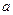
的取值范圍。
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
下列說法:①若
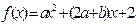
(其中
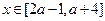
)是偶函數, 則實數
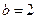
;
②
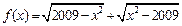
既是奇函數又是偶函數;
③已知
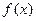
是定義在
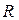
上的奇函數,若當
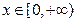
時,
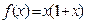
,則當
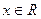
時,
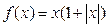
;
④已知
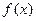
是定義在R上的不恒為零的函數, 且對任意的
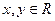
都滿足
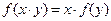
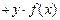
, 則
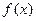
是奇函數.
其中所有正確說法的序號是
▲
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
已知函數
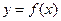
是定義在
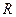
上的增函數,函數
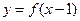
的圖象關于點

(1 , 0)對稱,若對任意的
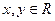
,不等式
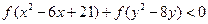
恒成立,則當
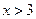
時,
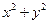
的取值范圍是
____▲_____
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
關于函數

,有下列命題:
①其圖象關于

軸對稱;
②當

時,

是增函數;當

時,

是減函數;
③

的最小值是

;
④

在區間(-1,0)、(2,+∞)上是增函數;
⑤

無最大值,也無最小值.
其中所有正確結論的序號是
.
查看答案和解析>>
主站蜘蛛池模板:
亚洲欧美综合精品久久成人
|
欧美亚洲国产一区
|
91视频精选|
色综合久|
91精品久久久久久久久久
|
91人人|
日韩欧美中文字幕在线视频
|
日本不卡一区二区
|
日韩2020狼一二三
|
黑人黄色毛片
|
黄色电影天堂
|
日韩免费福利视频
|
一区二区三区视频在线免费观看
|
国产精品久久免费看
|
久久久精品免费观看
|
天天摸天天操
|
超碰激情|
四影虎影ww4hu55.com
|
成年无码av片在线
|
日本黄色影片在线观看
|
亚洲精品影院
|
亚州av一区二区
|
欧美日韩国产一区二区三区
|
久久国产精品免费一区二区三区
|
国产精品美女久久久久久久久久久
|
久久叉
|
久久国产久
|
免费看片一区二区三区
|
国产激情第一页
|
黄色在线免费看
|
欧美一区二区在线
|
免费看国产片在线观看
|
成人久久久久爱
|
精品国产精品三级精品av网址
|
国产中文在线
|
国产精品久久久久无码av
|
欧美午夜一区二区福利视频
|
www.欧美|
久久精品一区二区三区四区毛片
|
国产精品久久久久久久久久久久久久
|
欧美国产精品一区
|

 且存在
且存在 使
使
 是R上的單調增函數;
是R上的單調增函數; 其中
其中 


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案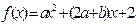 (其中
(其中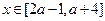 )是偶函數, 則實數
)是偶函數, 則實數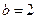 ;
;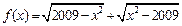 既是奇函數又是偶函數;
既是奇函數又是偶函數;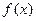 是定義在
是定義在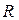 上的奇函數,若當
上的奇函數,若當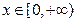 時,
時, 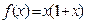 ,則當
,則當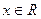 時,
時, 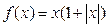 ;
;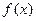 是定義在R上的不恒為零的函數, 且對任意的
是定義在R上的不恒為零的函數, 且對任意的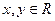 都滿足
都滿足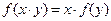
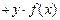 , 則
, 則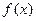 是奇函數.
是奇函數.  ,有下列命題:
,有下列命題: 軸對稱;
軸對稱; 時,
時, 是增函數;當
是增函數;當 時,
時, 是減函數;
是減函數; 的最小值是
的最小值是 ;
; 在區間(-1,0)、(2,+∞)上是增函數;
在區間(-1,0)、(2,+∞)上是增函數; 無最大值,也無最小值.
無最大值,也無最小值.