
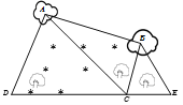
【題目】如圖,為了測量某濕地![]() 兩點間的距離,觀察者找到在同一直線上的三點
兩點間的距離,觀察者找到在同一直線上的三點![]() .從
.從![]() 點測得
點測得![]() ,從
,從![]() 點測得
點測得![]() ,
,![]() ,從
,從![]() 點測得
點測得![]() .若測得
.若測得![]() ,
,![]() (單位:百米),則
(單位:百米),則![]() 兩點的距離為( )
兩點的距離為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由已知易得∠EBC=180°﹣75°﹣60°=45°,再由正弦定理![]() 求得
求得![]() ,再由余弦定理AB2=AC2+BC2﹣2ACBCcos∠ACB=9,所以AB=3.
,再由余弦定理AB2=AC2+BC2﹣2ACBCcos∠ACB=9,所以AB=3.
根據題意,在△ADC中,∠ACD=45°,∠ADC=67.5°,DC=2![]() ,
,
則∠DAC=180°﹣45°﹣67.5°=67.5°,則AC=DC=2![]() ,
,
在△BCE中,∠BCE=75°,∠BEC=60°,CE![]() ,
,
則∠EBC=180°﹣75°﹣60°=45°,
則有![]() ,變形可得BC
,變形可得BC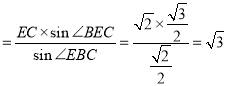 ,
,
在△ABC中,AC=2![]() ,BC
,BC![]() ,∠ACB=180°﹣∠ACD﹣∠BCE=60°,
,∠ACB=180°﹣∠ACD﹣∠BCE=60°,
則AB2=AC2+BC2﹣2ACBCcos∠ACB=9,
則AB=3;
故選:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,等腰梯形MNCD中,MD∥NC,MN=![]() MD=2,∠CDM=60°,E為線段MD上一點,且ME=3,以EC為折痕將四邊形MNCE折起,使MN到達AB的位置,且AE⊥DC
MD=2,∠CDM=60°,E為線段MD上一點,且ME=3,以EC為折痕將四邊形MNCE折起,使MN到達AB的位置,且AE⊥DC

(1)求證:DE⊥平面ABCE;
(2)求點A到平面DBE的距離
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 的焦點為
的焦點為![]() ,橢圓
,橢圓![]() 的中心在原點,
的中心在原點,![]() 為其右焦點,點
為其右焦點,點![]() 為曲線
為曲線![]() 和
和![]() 在第一象限的交點,且
在第一象限的交點,且![]() .
.

(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設![]() 為拋物線
為拋物線![]() 上的兩個動點,且使得線段
上的兩個動點,且使得線段![]() 的中點
的中點![]() 在直線
在直線![]() 上,
上,
![]() 為定點,求
為定點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有2位男生,3位女生去參加一個聯歡活動,該活動有甲、乙兩個項目可供參加者選擇.
(Ⅰ)為增加趣味性,約定:每個人通過擲一枚質地均勻的骰子決定自己去參加哪個項目聯歡,擲出點數為1或2的人去參加甲項目聯歡,擲出點數大于2的人去參加乙項目聯歡.求這5人中恰好有3人去參加甲項目聯歡的概率;
(Ⅱ)若從這5人中隨機選派3人去參加甲項目聯歡,設![]() 表示這3個人中女生的人數,求隨機變量
表示這3個人中女生的人數,求隨機變量![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設不等式![]() 確定的平面區域為U,
確定的平面區域為U,![]() 確定的平面區域為V.
確定的平面區域為V.
(1)定義橫、縱坐標為整數的點為“整點”,在區域U內任取3個整點,求這些整點中恰有2個整點在區域V內的概率;
(2)設集合![]() ;集合
;集合![]() 若從集合A到集合B可以建立m個不同的映射?從集合B到集合A可以建立n個不同的映射,求m,n的值.
若從集合A到集合B可以建立m個不同的映射?從集合B到集合A可以建立n個不同的映射,求m,n的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年12月18日上午10時,在人民大會堂舉行了慶祝改革開放40周年大會.40年眾志成城,40年砥礪奮進,40年春風化雨,中國人民用雙手書寫了國家和民族發展的壯麗史詩.會后,央視媒體平臺,收到了來自全國各地的紀念改革開放40年變化的老照片,并從眾多照片中抽取了100張照片參加“改革開放40年圖片展”,其作者年齡集中在![]() 之間,根據統計結果,做出頻率分布直方圖如下:
之間,根據統計結果,做出頻率分布直方圖如下:

(Ⅰ)求這100位作者年齡的樣本平均數![]() 和樣本方差
和樣本方差![]() (同一組數據用該區間的中點值作代表);
(同一組數據用該區間的中點值作代表);
(Ⅱ)由頻率分布直方圖可以認為,作者年齡X服從正態分布![]() ,其中
,其中![]() 近似為樣本平
近似為樣本平
均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() .
.
(i)利用該正態分布,求![]() ;
;
(ii)央視媒體平臺從年齡在![]() 和
和![]() 的作者中,按照分層抽樣的方法,抽出了7人參加“紀念改革開放40年圖片展”表彰大會,現要從中選出3人作為代表發言,設這3位發言者的年齡落在區間
的作者中,按照分層抽樣的方法,抽出了7人參加“紀念改革開放40年圖片展”表彰大會,現要從中選出3人作為代表發言,設這3位發言者的年齡落在區間![]() 的人數是Y,求變量Y的分布列和數學期望.附:
的人數是Y,求變量Y的分布列和數學期望.附:![]() ,若
,若![]() ,則
,則![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某食品廠為了檢查一條自動包裝流水線的生產情況,隨即抽取該流水線上![]() 件產品作為樣本算出他們的重量(單位:克)重量的分組區間為
件產品作為樣本算出他們的重量(單位:克)重量的分組區間為![]() ,
,![]() ,……
,……![]() ,由此得到樣本的頻率分布直方圖,如圖所示.
,由此得到樣本的頻率分布直方圖,如圖所示.
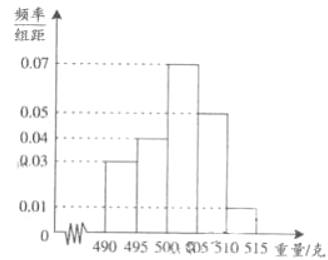
(1)根據頻率分布直方圖,求重量超過![]() 克的產品數量.
克的產品數量.
(2)在上述抽取的![]() 件產品中任取
件產品中任取![]() 件,設
件,設![]() 為重量超過
為重量超過![]() 克的產品數量,求
克的產品數量,求![]() 的分布列.
的分布列.
(3)從流水線上任取![]() 件產品,求恰有
件產品,求恰有![]() 件產品合格的重量超過
件產品合格的重量超過![]() 克的概率.
克的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com