【題目】已知函數
,其中
是實數。設
, 
為該函數圖象上的兩點,且
，若函數
的圖象在點
處的切線重合,則的取值范圍為（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
先根據導數的幾何意義寫出函數f（x）在點A、B處的切線方程，再利用兩直線重合的充要條件列出關系式，從而得出a=lnx2+（
﹣1）2﹣1，最后利用導數研究它的單調性和最值，即可得出a的取值范圍．
當x1＜x2＜0，或0＜x1＜x2時，f′（x1）≠f′（x2），故x1＜0＜x2，
當x1＜0時，函數f（x）在點A（x1，f（x1））處的切線方程為y﹣（x12+2x1+a）=（2x1+2）（x﹣x1）；
當x2＞0時，函數f（x）在點B（x2，f（x2））處的切線方程為y﹣lnx2=
（x﹣x2）；
兩直線重合的充要條件是=2x1+2①，lnx2﹣1=﹣x12+a②，
由①及x1＜0＜x2得0＜＜2，由①②得a=lnx2+（﹣1）2﹣1=﹣ln+
（﹣2）2﹣1，
令t=，則0＜t＜2，且a=t2﹣t﹣lnt，設h（t）=t2﹣t﹣lnt，（0＜t＜2）
則h′（t）=
t﹣1﹣
=
＜0，∴h（t）在（0，2）為減函數，
則h（t）＞h（2）=﹣ln2﹣1，∴a＞﹣ln2﹣1，
∴若函數f（x）的圖象在點A，B處的切線重合，a的取值范圍（﹣ln2﹣1，+∞）．
故選：A．
科目：高中數學 來源： 題型：
【題目】設函數
(
，
，
，
)的部分圖象如圖所示.
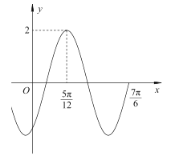
（1）求函數
的解析式；
（2）求函數的最小值及
取到最小值時自變量x的集合；
（3）將函數圖像上所有點的縱坐標不變，橫坐標變為原來的
(
)倍，得到函數
的圖象.若函數在區間
上恰有5個零點，求t的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知不交于同一點的三條直線
：4x＋y－4＝0，
：mx＋y＝0，
：x－my－4＝0.
(1)當這三條直線不能圍成三角形時，求實數m的值；
(2)當與，都垂直時，求兩垂足間的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司生產某種產品的速度為
千克/小時，每小時可獲得的利潤是
元，其中
.
（1）要使生產該產品每小時獲得的利潤為60元，求每小時生產多少千克?
（2）要使生產400千克該產品獲得的利潤最大，問：此公司每小時應生產多少千克產品?并求出最大利潤.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】20名學生某次數學考試成績(單位：分)的頻率分布直方圖如下：
(1)求頻率直方圖中a的值；
(2)分別求出成績落在[50,60)與[60,70)中的學生人數；
(3)從成績在[50,70)的學生中人選2人，求這2人的成績都在[60,70)中的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數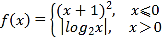
，若方程f（x）＝a有四個不同的解x1，x2，x3，x4，且x1＜x2＜x3＜x4，則
的取值范圍為（ ）
A. （﹣1，+∞）B. （﹣1，1]C. （﹣∞，1）D. [﹣1，1）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
