
【題目】已知函數f(x)=x2+2bx+5(b∈R).
(1)若b=2,試解不等式f(x)<10;
(2)若f(x)在區間[﹣4,﹣2]上的最小值為﹣11,試求b的值;
(3)若|f(x)﹣5|≤1在區間(0,1)上恒成立,試求b的取值范圍.
【答案】
(1)解:f(x)=x2+4x+5<10,
即x2+4x﹣5<0,
即(x+5)(x﹣1)<0,
解得﹣5<x<1,
故不等式的解集為(﹣5,1)
(2)解:f(x)=x2+2bx+5=(x+b)2﹣b2+5,
其對稱軸為x=﹣b,
當b<﹣4時,在區間[﹣4,﹣2]上單調遞增,故ymin=16﹣8x+5=﹣11,解得b=4,舍去
當﹣4≤b≤﹣2時,在對稱軸處取最小值,故ymin=﹣b2+5=﹣11,解得b=﹣4,
當b>﹣2時,在區間[﹣4,﹣2]上單調遞減,故ymin=4﹣4b+5=﹣11,解得b=5,
綜上所述:b的值為﹣4或5
(3)解:|f(x)﹣5|≤1在區間(0,1)上恒成立,
∴|x2+bx|≤1在區間(0,1)上恒成立,
∴﹣1≤x2+2bx≤1,
∴﹣x﹣ ![]() ≤2b≤﹣x+
≤2b≤﹣x+ ![]()
∵函數y=﹣x﹣ ![]() 在(0,1)上為增函數,y>﹣1﹣1=﹣2,
在(0,1)上為增函數,y>﹣1﹣1=﹣2,
函數y=﹣x+ ![]() 在(0,1)上為減函數,y<﹣1+1=0,
在(0,1)上為減函數,y<﹣1+1=0,
∴﹣2≤2b≤0,
解得﹣1≤b≤0,
故b的取值范圍為[﹣1.0]
【解析】(1)根據一元二次不等式的解法解得即可.(2)根據所給的二次函數的性質,寫出對于對稱軸所在的區間不同時,對應的函數的最小值,(3)利用函數的單調性分別求出y= ![]() ﹣x 的最小值為0,y=﹣x﹣
﹣x 的最小值為0,y=﹣x﹣ ![]() 的最大值為﹣2,由此求得b的取值范圍.
的最大值為﹣2,由此求得b的取值范圍.
【考點精析】根據題目的已知條件,利用二次函數的性質的相關知識可以得到問題的答案,需要掌握當![]() 時,拋物線開口向上,函數在
時,拋物線開口向上,函數在![]() 上遞減,在
上遞減,在![]() 上遞增;當
上遞增;當![]() 時,拋物線開口向下,函數在
時,拋物線開口向下,函數在![]() 上遞增,在
上遞增,在![]() 上遞減.
上遞減.


 學習實踐園地系列答案
學習實踐園地系列答案科目:高中數學 來源: 題型:
【題目】如圖![]() 是直三棱柱,底面
是直三棱柱,底面![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,直三棱柱的高等于4,線段
,直三棱柱的高等于4,線段![]() 的中點為
的中點為![]() ,線段
,線段![]() 的中點為
的中點為![]() ,線段
,線段![]() 的中點為
的中點為![]() .
.
(1)求異面直線![]() 、
、![]() 所成角的大小;
所成角的大小;
(2)求三棱錐![]() 的體積.
的體積.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log22x﹣mlog2x+2,其中m∈R.
(1)當m=3時,求方程f(x)=0的解;
(2)當x∈[1,2]時,求f(x)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 上的任一點到焦點的距離最大值為3,離心率為
上的任一點到焦點的距離最大值為3,離心率為![]() ,
,
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 為曲線
為曲線![]() 上兩點,
上兩點, ![]() 為坐標原點,直線
為坐標原點,直線![]() 的斜率分別為
的斜率分別為![]() ,且
,且![]() ,求直線
,求直線![]() 被圓
被圓![]() 截得弦長的最大值及此時直線
截得弦長的最大值及此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,x∈R,a∈R.
,x∈R,a∈R.
(1)a=1時,求證:f(x)在區間(﹣∞,0)上為單調增函數;
(2)當方程f(x)=3有解時,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某農科所發現,一種作物的年收獲量 ![]() (單位:
(單位: ![]() )與它“相近”作物的株數
)與它“相近”作物的株數 ![]() 具有線性相關關系(所謂兩株作物“相近”是指它們的直線距離不超過
具有線性相關關系(所謂兩株作物“相近”是指它們的直線距離不超過 ![]() ),并分別記錄了相近作物的株數為
),并分別記錄了相近作物的株數為 ![]() 時,該作物的年收獲量的相關數據如下:
時,該作物的年收獲量的相關數據如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)求該作物的年收獲量 ![]() 關于它“相近”作物的株數
關于它“相近”作物的株數![]() 的線性回歸方程;
的線性回歸方程;
(2)農科所在如圖所示的正方形地塊的每個格點(指縱、橫直線的交叉點)處都種了一株該作物,其中每
個小正方形的面積為 ![]() ,若在所種作物中隨機選取一株,求它的年收獲量的分布列與數學期望.(注:年收
,若在所種作物中隨機選取一株,求它的年收獲量的分布列與數學期望.(注:年收
獲量以線性回歸方程計算所得數據為依據)
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估
的斜率和截距的最小二乘估
計分別為, 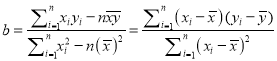 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三共有800名學生,為了解學生3月月考生物測試情況,根據男女學生人數差異較大,從中隨機抽取了200名學生,記錄他們的分數,并整理得如圖頻率分布直方圖.
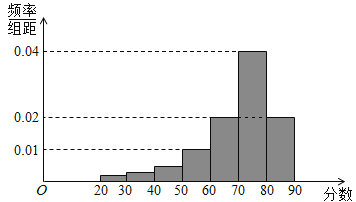
(1)若成績不低于60分的為及格,成績不低于80分的為優秀,試估計總體中合格的有多少人?優秀的有多少人?
(2)已知樣本中有一半的女生分數不小于80,且樣本中不低于80分的男女生人數之比2:3,試估計總體中男生和女生人數的比例.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,江的兩岸可近似地看出兩條平行的直線,江岸的一側有![]() ,
, ![]() 兩個蔬菜基地,江岸的另一側點
兩個蔬菜基地,江岸的另一側點![]() 處有一個超市.已知
處有一個超市.已知![]() 、
、![]() 、
、![]() 中任意兩點間的距離為
中任意兩點間的距離為![]() 千米,超市欲在
千米,超市欲在![]() 之間建一個運輸中轉站
之間建一個運輸中轉站![]() ,
, ![]() ,
, ![]() 兩處的蔬菜運抵
兩處的蔬菜運抵![]() 處后,再統一經過貨輪運抵
處后,再統一經過貨輪運抵![]() 處,由于
處,由于![]() ,
, ![]() 兩處蔬菜的差異,這兩處的運輸費用也不同.如果從
兩處蔬菜的差異,這兩處的運輸費用也不同.如果從![]() 處出發的運輸費為每千米
處出發的運輸費為每千米![]() 元.從
元.從![]() 處出發的運輸費為每千米
處出發的運輸費為每千米![]() 元,貨輪的運輸費為每千米
元,貨輪的運輸費為每千米![]() 元.
元.

(1)設![]() ,試將運輸總費用
,試將運輸總費用![]() (單位:元)表示為
(單位:元)表示為![]() 的函數
的函數![]() ,并寫出自變量的取值范圍;
,并寫出自變量的取值范圍;
(2)問中轉站![]() 建在何處時,運輸總費用
建在何處時,運輸總費用![]() 最小?并求出最小值.
最小?并求出最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x2≥1}, ![]() ,則A∩(RB)=( )
,則A∩(RB)=( )
A.(2,+∞)
B.(﹣∞,﹣1]∪(2,+∞)
C.(﹣∞,﹣1)∪(2,+∞)
D.[﹣1,0]∪[2,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com