
【題目】將函數y=sinx的圖象上所有點的橫坐標縮小到原來的 ![]() (縱坐標不變),再將所得到的圖象上所有點向左平移
(縱坐標不變),再將所得到的圖象上所有點向左平移 ![]() 個單位,所得函數圖象的解析式為( )
個單位,所得函數圖象的解析式為( )
A.y=sin(2x﹣ ![]() )
)
B.y=sin(2x+ ![]() )
)
C.y=sin( ![]() x+
x+ ![]() )
)
D.y=sin( ![]() x+
x+ ![]() )
)
 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,E、F、G分別是棱A1B1、BB1、B1C1的中點,則下列結論中:
①FG⊥BD
②B1D⊥面EFG
③面EFG∥面ACC1A1
④EF∥面CDD1C1
正確結論的序號是( )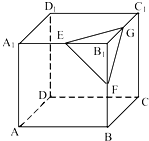
A.①和②
B.②和④
C.①和③
D.③和④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明同學在寒假社會實踐活動中,對白天平均氣溫與某家奶茶店的![]() 品牌飲料銷量之間的關系進行了分析研究,他分別記錄了1月11日至1月15日的白天氣溫
品牌飲料銷量之間的關系進行了分析研究,他分別記錄了1月11日至1月15日的白天氣溫![]() (
(![]() )與該奶茶店的
)與該奶茶店的![]() 品牌飲料銷量
品牌飲料銷量![]() (杯),得到如表數據:
(杯),得到如表數據:
日期 | 1月11號 | 1月12號 | 1月13號 | 1月14號 | 1月15號 |
平均氣溫 | 9 | 10 | 12 | 11 | 8 |
銷量 | 23 | 25 | 30 | 26 | 21 |
(1)若先從這五組數據中抽出2組,求抽出的2組數據恰好是相鄰2天數據的概率;
(2)請根據所給五組數據,求出![]() 關于
關于![]() 的線性回歸方程式
的線性回歸方程式![]() ;
;
(3)根據(2)所得的線性回歸方程,若天氣預報1月16號的白天平均氣溫為![]() ,請預測該奶茶店這種飲料的銷量.
,請預測該奶茶店這種飲料的銷量.
(參考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
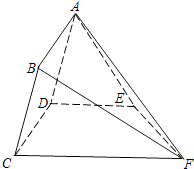
【題目】如圖,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2, ![]() ,CF=6,∠CFE=45°.
,CF=6,∠CFE=45°.
(Ⅰ)求證:BF∥平面ADE;
(Ⅱ)在線段CF上求一點G,使銳二面角B﹣EG﹣D的余弦值為 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐的側棱PD⊥底面ABCD,且底面ABCD是直角梯形,AD⊥CD,AB∥CD,AB=AD= ![]() CD=2,點M在側棱上.
CD=2,點M在側棱上.
(1)求證:BC⊥平面BDP;
(2)若側棱PC與底面ABCD所成角的正切值為 ![]() ,點M為側棱PC的中點,求異面直線BM與PA所成角的余弦值.
,點M為側棱PC的中點,求異面直線BM與PA所成角的余弦值. 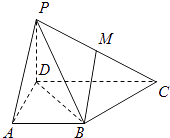
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,A,B兩點5條連線并聯,它們在單位時間內能通過的最大信息量依次為2,3,4,3,2.現記從中任取三條線且在單位時間內都通過的最大信息總量為ξ,則P(ξ≥8)= . 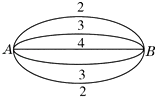
查看答案和解析>>
科目:高中數學 來源: 題型:
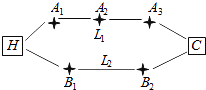
【題目】如圖,李先生家住H小區,他工作在C科技園區,從家開車到公司上班路上有L1、L2兩條路線,L1路線上有A1、A2、A3三個路口,各路口遇到紅燈的概率均為 ![]() ;L2路線上有B1、B2兩個路口,各路口遇到紅燈的概率依次為
;L2路線上有B1、B2兩個路口,各路口遇到紅燈的概率依次為 ![]() ,
, ![]() .
. 
(1)若走L1路線,求最多遇到1次紅燈的概率;
(2)若走L2路線,求遇到紅燈次數X的數學期望;
(3)按照“平均遇到紅燈次數最少”的要求,請你幫助李先生從上述兩條路線中選擇一條最好的上班路線,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
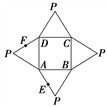
【題目】如圖是一幾何體的平面展開圖,其中ABCD為正方形,E,F分別為PA,PD的中點,
在此幾何體中,給出下面四個結論:
①直線BE與直線CF異面; ②直線BE與直線AF異面;
③直線EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正確的有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com