解析:已知|a|與|b|,求a·b只需確定其夾角θ,需注意到a∥b時,有〈a,b〉=0和〈a,b〉=π兩種可能.
解:(1)∵a∥b,
∴a、b的夾角有兩種情況,
即〈a,b〉=0或〈a,b〉=π.
于是〈a,b〉=0時,a·b=|a|·|b|cos〈a,b〉=4×5×cosθ=20,
〈a,b〉=π時,a·b=|a|·|b|cos〈a,b〉=4×5×cosπ=-20.
(2)a⊥b時,〈a,b〉=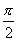 ,∴a·b=|a|·|b|cos
,∴a·b=|a|·|b|cos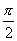 =0.
=0.
(3)〈a,b〉=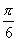 時,a·b=|a|·|b|·cos〈a,b〉=5×4×cos
時,a·b=|a|·|b|·cos〈a,b〉=5×4×cos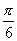 =
=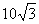 .
.

 閱讀快車系列答案
閱讀快車系列答案