
如圖,已知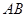 ⊥平面
⊥平面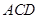 ,
,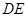 ∥
∥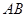 ,
,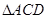 是正三角形,
是正三角形,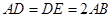 ,且
,且 是
是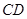 的中點.
的中點.

(Ⅰ)求證: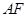 ∥平面
∥平面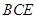 ;
;
(Ⅱ)求證:平面BCE⊥平面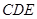 .
.
(1)取CE中點P,連結FP、BP,∵F為CD的中點,借助于中位線定理得到FP∥DE,再結合平行的傳遞性得到證明。
(2)對于面面垂直的證明,關鍵是要根據線面垂直的判定定理以及面面垂直的判定定理得到。
【解析】
試題分析:解:(Ⅰ)取CE中點P,連結FP、BP,
∵F為CD的中點,
∴FP∥DE,且FP=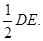
又AB∥DE,且AB=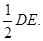 ∴AB∥FP,且AB=FP,
∴AB∥FP,且AB=FP,
∴ABPF為平行四邊形,∴AF∥BP. 4分
又∵AF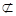 平面BCE,BP
平面BCE,BP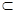 平面BCE,
平面BCE,
∴AF∥平面BCE …………7分
(Ⅱ)∵△ACD為正三角形,∴AF⊥CD
∵AB⊥平面ACD,DE//AB
∴DE⊥平面ACD 又AF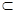 平面ACD
平面ACD
∴DE⊥AF
又AF⊥CD,CD∩DE=D
∴AF⊥平面CDE 12分
又BP∥AF
∴BP⊥平面CDE又∵BP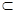 平面BCE
平面BCE
∴平面BCE⊥平面CDE 14分
考點:線面垂直和面面垂直
點評:主要是考查了空間中線面和面面垂直的判定定理的運用,屬于中檔題。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
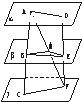 如圖,已知平面α∥平面β∥平面γ,且β位于α與γ之間.點A、D∈α,C、F∈γ,
如圖,已知平面α∥平面β∥平面γ,且β位于α與γ之間.點A、D∈α,C、F∈γ,| AB |
| BC |
| DE |
| EF |
| h′ |
| h |
查看答案和解析>>
科目:高中數學 來源: 題型:
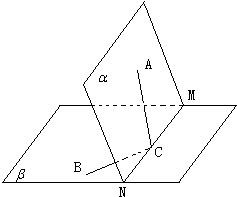 如圖,已知平面α∩平面β=MN,A∈α,B∈β,C∈MN且∠ACM=60°,∠BCN=45°,二面角A-MN-B=60°,AC=2.
如圖,已知平面α∩平面β=MN,A∈α,B∈β,C∈MN且∠ACM=60°,∠BCN=45°,二面角A-MN-B=60°,AC=2.查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•青州市模擬)如圖,已知平面BCC1B1是圓柱的軸截面(經過圓柱的軸的截面),BC是圓柱底面的直徑,O為底面圓心,E為母線CC1的中點,已知AB=AC=AA1=4.
(2012•青州市模擬)如圖,已知平面BCC1B1是圓柱的軸截面(經過圓柱的軸的截面),BC是圓柱底面的直徑,O為底面圓心,E為母線CC1的中點,已知AB=AC=AA1=4.查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•溫州一模)如圖,已知平面QBC與直線PA均垂直于Rt△ABC所在平面,且PA=AB=AC,
(2013•溫州一模)如圖,已知平面QBC與直線PA均垂直于Rt△ABC所在平面,且PA=AB=AC,查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•寧德模擬)如圖,已知平面AEMN丄平面ABCD,四邊形AEMN為 正方形,四邊形ABCD為直角梯形,AB∥CD,∠ABC=90°,BC=CD=2AB=2,E 為 CD 的中點.
(2013•寧德模擬)如圖,已知平面AEMN丄平面ABCD,四邊形AEMN為 正方形,四邊形ABCD為直角梯形,AB∥CD,∠ABC=90°,BC=CD=2AB=2,E 為 CD 的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com