
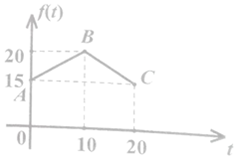
 經過市場調查,某門市部的一種小商品在過去的20天內的銷售量(件)與價格(元)均為時間t (天)的函數,且日銷售量近似滿足g(t)=80-2t (件),而日銷售量價格近似滿足函數f(t),且f(t)的圖象為如圖所示的兩線段AB,BC.
經過市場調查,某門市部的一種小商品在過去的20天內的銷售量(件)與價格(元)均為時間t (天)的函數,且日銷售量近似滿足g(t)=80-2t (件),而日銷售量價格近似滿足函數f(t),且f(t)的圖象為如圖所示的兩線段AB,BC.分析 (1)日銷售額=銷售量×價格,根據條件寫成分段函數即可;
(2)分別求出函數在各段的最大值、最小值,取其中最小者為最小值,最大者為最大值;
解答 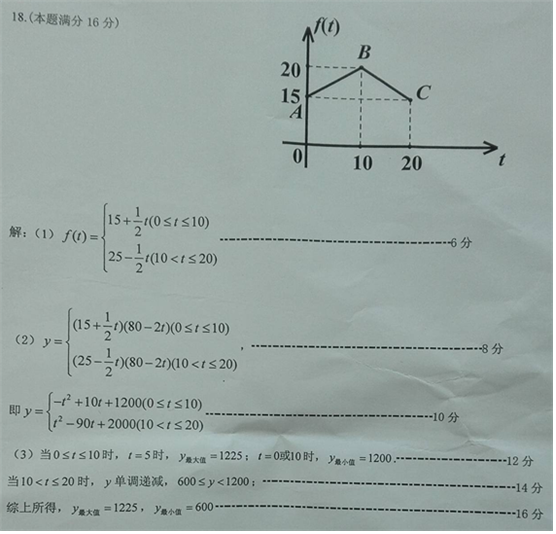 解:(1)f(t)=$\left\{\begin{array}{l}{15+\frac{1}{2}t,0≤t≤10}\\{25-\frac{1}{2}t,10<t≤20}\end{array}\right.$
解:(1)f(t)=$\left\{\begin{array}{l}{15+\frac{1}{2}t,0≤t≤10}\\{25-\frac{1}{2}t,10<t≤20}\end{array}\right.$
(2)y=
(2)當1≤t<10時,可得t=1時ymin=1209;t=5時ymax=1225…(9分)
當10≤t≤20時,可得t=10時ymax=1200;t=20時ymin=600…(12分)
因此,該商品在第5天可取得日銷售額y的最大值1225元;
第20天,日銷售額y取得最小值600元…(14分)
點評 本題考查函數在實際問題中的應用,考查分段函數最值的求法,考查學生解決實際問題的能力,屬中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在三棱錐P-ABC中,△ABC是等邊三角形,D是AC的中點,PA=PC,二面角P-AC-B的大小為60°;
如圖,在三棱錐P-ABC中,△ABC是等邊三角形,D是AC的中點,PA=PC,二面角P-AC-B的大小為60°;查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | B. | $\frac{2}{3}$$\overrightarrow{b}$+$\frac{5}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com