
已知函數 ,其中
,其中 是實數,設
是實數,設 為該函數的圖象上的兩點,且
為該函數的圖象上的兩點,且 .
.
⑴指出函數 的單調區間;
的單調區間;
⑵若函數 的圖象在點
的圖象在點 處的切線互相垂直,且
處的切線互相垂直,且 ,求
,求 的最小值;
的最小值;
⑶若函數 的圖象在點
的圖象在點 處的切線重合,求
處的切線重合,求 的取值范圍.
的取值范圍.
(1)單調減區間為 ,單調增區間為
,單調增區間為 ;(2)1;(3)
;(2)1;(3) .
.
解析試題分析:(1)根據基本初等函數的性質知,分段函數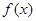 在
在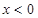 時是二次函數的一部分,有兩個單調區間:增區間
時是二次函數的一部分,有兩個單調區間:增區間 ,減區間
,減區間 ,
, 時是對數函數,只有一個單調增區間
時是對數函數,只有一個單調增區間 ;(2)對函數圖象來講,它在某點處的切線斜率等于該函數在此點處的導數,故有
;(2)對函數圖象來講,它在某點處的切線斜率等于該函數在此點處的導數,故有 ,由于
,由于 ,
, 兩點在
兩點在 軸的左邊,
軸的左邊, ,因此有
,因此有 ,顯然有
,顯然有 ,
, 可以表示為關于
可以表示為關于 的函數,從而求出最小值(
的函數,從而求出最小值( ,
,
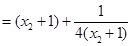 應用基本不等式即可得解)也可以直接湊配出基本不等式的形式,
應用基本不等式即可得解)也可以直接湊配出基本不等式的形式, =
= 利用基本不等式);(3)這里我們首先分析
利用基本不等式);(3)這里我們首先分析 所處范圍,結合圖象易知
所處范圍,結合圖象易知 不可能在同一單調區間,只能是
不可能在同一單調區間,只能是 ,那么我們可得出
,那么我們可得出 兩點處的切線方程分別為
兩點處的切線方程分別為 ,
, ,兩條切線相同,則有
,兩條切線相同,則有 ,于是可把
,于是可把 表示為
表示為 (或者
(或者 )的函數,把求
)的函數,把求 匠范圍轉化為求函數的值域.
匠范圍轉化為求函數的值域.
試題解析:(1)單調減區間為 ,單調增區間為
,單調增區間為 4分
4分
(2) ,
,
當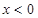 時,因為
時,因為 ,所以
,所以 .8分
.8分
∴
當且僅當 時等號成立,
時等號成立,
∴ 的最小值為1.10分
的最小值為1.10分
(3)當 或
或 時,
時, ,故
,故
當 時,函數
時,函數 的圖象在點
的圖象在點 的切線方程為
的切線方程為
即
當 時,函數
時,函數 在
在 切線方程為
切線方程為
兩切線重合的充要條件是 13分
13分
由①及 知
知
由①②得
又 ,與
,與 在
在 都為減函數.
都為減函數.
∴ 16分
16分
考點:(1)單調區間;(2)函數圖象的切線及基本不等式;(3)切線與函數的值域.


 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:解答題
已知函數f(x)=x3+ax-2,(a R).
R).
(l)若f(x)在區間(1,+ )上是增函數,求實數a的取值范圍;
)上是增函數,求實數a的取值范圍;
(2)若 ,且f(x0)=3,求x0的值;
,且f(x0)=3,求x0的值;
(3)若 ,且在R上是減函數,求實數a的取值范圍。
,且在R上是減函數,求實數a的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
湖南省環保研究所對長沙市中心每天環境放射性污染情況進行調查研究后,發現一天中環境綜合放射性污染指數 與時刻x的關系為
與時刻x的關系為 ,其中a是與氣象有關的參數,且
,其中a是與氣象有關的參數,且 ,若用每天
,若用每天 的最大值作為當天的綜合放射性污染指數,并記作
的最大值作為當天的綜合放射性污染指數,并記作 .
.
(Ⅰ)令 ,求t的取值范圍;
,求t的取值范圍;
(Ⅱ)省政府規定,每天的綜合放射性污染指數不得超過2,試問目前市中心的綜合放射性污染指數是否超標?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某建筑公司要在一塊寬大的矩形地面(如圖所示)上進行開發建設,陰影部分為一公共設施建設不能開發,且要求用欄柵隔開(欄柵要求在一直線上),公共設施邊界為曲線 的一部分,欄柵與矩形區域的邊界交于點
的一部分,欄柵與矩形區域的邊界交于點 ,交曲線于點
,交曲線于點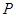 ,設
,設 .
.
(1)將△ (
( 為坐標原點)的面積
為坐標原點)的面積 表示成
表示成 的函數
的函數 ;
;
(2)若在 處,
處, 取得最小值,求此時
取得最小值,求此時 的值及
的值及 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com