
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() :
:![]() 的右頂點與拋物線
的右頂點與拋物線![]() :
:![]() 的焦點
的焦點![]() 重合,其離心率
重合,其離心率![]() .過
.過![]() 作兩條相互垂直的直線
作兩條相互垂直的直線![]() 與
與![]() ,且
,且![]() 交拋物線
交拋物線![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 交橢圓
交橢圓![]() 于另一點
于另一點![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 面積的最小值.
面積的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由拋物線的方程可得焦點![]() 的坐標,由題意可得橢圓的
的坐標,由題意可得橢圓的![]() 值,再由離心率可得
值,再由離心率可得![]() 的值,再由
的值,再由![]() 之間的關系求出
之間的關系求出![]() 的值,進而求出橢圓的方程;由題意可得直線
的值,進而求出橢圓的方程;由題意可得直線![]() 的斜率不為
的斜率不為![]() ,設直線
,設直線![]() 的方程與拋物線聯立求出兩根之積,進而求出數量積
的方程與拋物線聯立求出兩根之積,進而求出數量積 ![]() 的值;
的值;
(2)由(1)可得弦長![]() 表達式,當直線
表達式,當直線![]() 垂直于
垂直于![]() 軸時,由題意可得直線
軸時,由題意可得直線![]() 為
為![]() 軸,與橢圓的另一個交點為橢圓的左頂點,求出三角形
軸,與橢圓的另一個交點為橢圓的左頂點,求出三角形![]() 的面積,當直線
的面積,當直線![]() 不垂直于
不垂直于![]() 軸時,設直線
軸時,設直線![]() 的方程與橢圓聯立求出
的方程與橢圓聯立求出![]() 的坐標,由面積公式可得面積的表達式,換元,求導,由函數的單調性求出三角形
的坐標,由面積公式可得面積的表達式,換元,求導,由函數的單調性求出三角形![]() 面積的最小值.
面積的最小值.
(1)由拋物線的方程可得焦點![]() ,由題意可得橢圓的右頂點的坐標為
,由題意可得橢圓的右頂點的坐標為![]() 即
即![]() , 又離心率
, 又離心率![]() ,可得
,可得![]() ,所以
,所以![]() ,
,
所以橢圓![]() 的方程為:
的方程為:![]() ,
,
由![]() 交拋物線
交拋物線![]() 于
于![]() 兩點可得直線
兩點可得直線![]() 的斜率不為
的斜率不為![]() ,
,
設![]() 的方程為:
的方程為:![]() ,設
,設![]() ,
,
直線與拋物線聯立![]() ,整理可得
,整理可得![]() ,
,
所以![]() ,
,
所以![]() ;
;
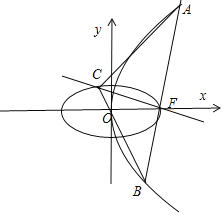
(2)由(1)知![]()
![]() ,
,
當![]() 時,
時,![]() ,由題意可得
,由題意可得![]() ,所以
,所以![]() ;
;
當![]() ,設直線
,設直線![]() 的方程為:
的方程為:![]() ,代入橢圓的方程可得
,代入橢圓的方程可得![]() ,
,
可得![]() ,
,
所以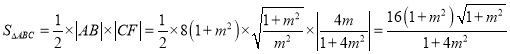 , 令
, 令![]() ,則
,則![]() ,
,
令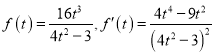 ,
,
令![]() ,可得
,可得![]() ,
,
當![]() ,
,![]() ,
,![]() 單調遞減,
單調遞減,
當![]() ,
,![]() ,
,![]() 單調遞增,
單調遞增,
所以![]() ,
,
故![]() ,當且僅當
,當且僅當![]() 時取等號,
時取等號,
綜上所述![]() 面積的最小值為
面積的最小值為![]() .
.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目:高中數學 來源: 題型:
【題目】某工廠的某種產品成箱包裝,每箱200件,每一箱產品在交付用戶之前要對產品作檢驗,如檢驗出不合格品,則更換為合格品.檢驗時,先從這箱產品中任取20件作檢驗,再根據檢驗結果決定是否對余下的所有產品作檢驗,設每件產品為不合格品的概率都為![]() ,且各件產品是否為不合格品相互獨立.
,且各件產品是否為不合格品相互獨立.
(1)記20件產品中恰有2件不合格品的概率為![]() ,求
,求![]() 的最大值點
的最大值點![]() .
.
(2)現對一箱產品檢驗了20件,結果恰有2件不合格品,以(1)中確定的![]() 作為
作為![]() 的值.已知每件產品的檢驗費用為2元,若有不合格品進入用戶手中,則工廠要對每件不合格品支付25元的賠償費用.
的值.已知每件產品的檢驗費用為2元,若有不合格品進入用戶手中,則工廠要對每件不合格品支付25元的賠償費用.
(i)若不對該箱余下的產品作檢驗,這一箱產品的檢驗費用與賠償費用的和記為![]() ,求
,求![]() ;
;
(ii)以檢驗費用與賠償費用和的期望值為決策依據,是否該對這箱余下的所有產品作檢驗?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年1月底因新型冠狀病毒感染的肺炎疫情形勢嚴峻,避免外出是減少相互交叉感染最有效的方式.在家中適當鍛煉,合理休息,能夠提高自身免疫力,抵抗該種病毒.某小區為了調查“宅”家居民的運動情況,從該小區隨機抽取了100位成年人,記錄了他們某天的鍛煉時間,其頻率分布直方圖如下:
(1)求a的值,并估計這100位居民鍛煉時間的平均值![]() (同一組中的數據用該組區間的中點值代表);
(同一組中的數據用該組區間的中點值代表);
(2)小張是該小區的一位居民,他記錄了自己“宅”家7天的鍛煉時長:
序號n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
鍛煉時長m(單位:分鐘) | 10 | 15 | 12 | 20 | 30 | 25 | 35 |
(Ⅰ)根據數據求m關于n的線性回歸方程;
(Ⅱ)若![]() (
(![]() 是(1)中的平均值),則當天被稱為“有效運動日”.估計小張“宅”家第8天是否是“有效運動日”?
是(1)中的平均值),則當天被稱為“有效運動日”.估計小張“宅”家第8天是否是“有效運動日”?
附;在線性回歸方程![]() 中,
中,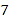 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在傳染病學中,通常把從致病刺激物侵入機體或者對機體發生作用起,到機體出現反應或開始呈現該疾病對應的相關癥狀時止的這一階段稱為潛伏期.
(1)一研究團隊統計了某地區1000名患者的相關信息,得到如下表格,

該傳染病的潛伏期受諸多因素影響,為研究潛伏期與患者年齡的關系,以潛伏期是否超過6天為標準進行分層抽樣,從上述1000名患者中抽取200人,得到如下列聯表,請將列聯表補充完整,并根據列聯表判斷是否有95%的把握認為潛伏期與患者年齡有關
潛伏期≤6天 | 潛伏期>6天 | 總計 | |
50歲以上(含50歲) | 100 | ||
50歲以下 | 55 | ||
總計 | 200 |
(2)以這1000名患者的潛伏期超過6天的頻率,代替該地區1名患者潛伏期超過6天發生的概率,每名患者的潛伏期是否超過6天相互獨立.為了深入研究,該研究團隊隨機調查了20名患者,其中潛伏期超過6天的人數最有可能(即概率最大)是多少?
附:下面的臨界值表僅供參考.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
(參考公式: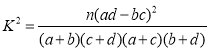 ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的右焦點為
的右焦點為![]() ,過焦點
,過焦點![]() ,斜率為
,斜率為![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 、
、![]() 兩點(異于長軸端點),
兩點(異于長軸端點),![]() 是直線
是直線![]() 上的動點.
上的動點.

(1)若直線![]() 平分線段
平分線段![]() ,求證:
,求證:![]() .
.
(2)若直線![]() 的斜率
的斜率![]() ,直線
,直線![]() 、
、![]() 、
、![]() 的斜率成等差數列,求實數
的斜率成等差數列,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com