
【題目】如圖,在平面直角坐標系中,以原點為圓心,單位長度為半徑的圓上有兩點A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ). (Ⅰ)求
). (Ⅰ)求 ![]() ,
, ![]() 夾角的余弦值;
夾角的余弦值;
(Ⅱ)已知C(1,0),記∠AOC=α,∠BOC=β,求tan ![]() 的值.
的值.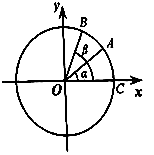
【答案】解:(Ⅰ)在平面直角坐標系中,以原點為圓心,單位長度為半徑的圓上有兩點 A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ),
),
∴ ![]() =(
=( ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ),|
),| ![]() |=|
|=| ![]() |=1,
|=1,
∴ ![]() ,
, ![]() 夾角的余弦值cos∠AOB=
夾角的余弦值cos∠AOB=  =
=  =
= ![]() .
.
(Ⅱ)設∠AOB的平分線OD交單位圓于點D,則∠COD= ![]() ,
,
從而D(cos ![]() ,sin
,sin ![]() ),∴
),∴ ![]() =(cos
=(cos ![]() ,sin
,sin ![]() ),
),
連接AB,可知OD⊥AB,即 ![]() =0.
=0.
∴ ![]() =
= ![]() ﹣
﹣ ![]() =(﹣
=(﹣ ![]() ,
, ![]() ),
),
∴(cos ![]() ,sin
,sin ![]() )(﹣
)(﹣ ![]() ,
, ![]() )=﹣
)=﹣ ![]() cos
cos ![]() +
+ ![]() sin
sin ![]() =0,
=0,
∴tan ![]() =
= ![]() .
.
【解析】(Ⅰ)先求出向量 ![]() ,
, ![]() 的坐標,再跟它們的夾角的余弦值cos∠AOB=
的坐標,再跟它們的夾角的余弦值cos∠AOB=  ,計算求得結果.(Ⅱ)設∠AOB的平分線OD交單位圓于點D,則∠COD=
,計算求得結果.(Ⅱ)設∠AOB的平分線OD交單位圓于點D,則∠COD= ![]() ,求得
,求得 ![]() 的坐標,根據
的坐標,根據 ![]() =0,求得tan
=0,求得tan ![]() 的值.
的值.
【考點精析】掌握數量積表示兩個向量的夾角和兩角和與差的正切公式是解答本題的根本,需要知道設![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 與
與![]() 的夾角,則;兩角和與差的正切公式:
的夾角,則;兩角和與差的正切公式:![]() .
.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(Ⅰ)若曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直,求函數
垂直,求函數![]() 的極值;
的極值;
(Ⅱ)設函數![]() .當
.當![]() 時,若區間
時,若區間![]() 上存在
上存在![]() ,使得
,使得![]() ,求實數
,求實數![]() 的取值范圍.(
的取值范圍.(![]() 為自然對數底數)
為自然對數底數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側棱AA1⊥底面ABC,AB=AC,D,D1分別是線段BC,B1C1的中點,P是線段AD上異于端點的點. 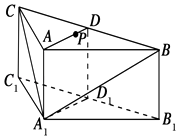
(1)在平面ABC內,試作出過點P與平面A1BC平行的直線l,并說明理由;
(2)證明:直線l⊥平面ADD1A1 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() .
.
(1)當 ![]() 時,求函數f(x)的取值范圍;
時,求函數f(x)的取值范圍;
(2)將f(x)的圖象向左平移 ![]() 個單位得到函數g(x)的圖象,求g(x)的單調遞增區間.
個單位得到函數g(x)的圖象,求g(x)的單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,銳角△ABC中, ![]() =
= ![]() ,
, ![]() =
= ![]() ,點M為BC的中點. (Ⅰ)試用
,點M為BC的中點. (Ⅰ)試用 ![]() ,
, ![]() 表示
表示 ![]() ;
;
(Ⅱ)若| ![]() |=5,|
|=5,| ![]() |=3,sin∠BAC=
|=3,sin∠BAC= ![]() ,求中線AM的長.
,求中線AM的長.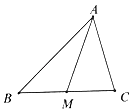
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個口袋內有4個不同的紅球,6個不同的白球,
(1)從中任取4個球,紅球的個數不比白球少的取法有多少種?
(2)若取一個紅球記2分,取一個白球記1分,從中任取5個球,使總分不少于7分的取法有多少種?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣a2x2+ax(a∈R).
(1)當a=1時,求函數f(x)最大值;
(2)若函數f(x)在區間(1,+∞)上是減函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某媒體為調查喜愛娛樂節目![]() 是否與觀眾性別有關,隨機抽取了30名男性和30名女性觀眾,抽查結果用等高條形圖表示如圖:
是否與觀眾性別有關,隨機抽取了30名男性和30名女性觀眾,抽查結果用等高條形圖表示如圖:
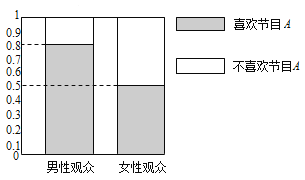
(1)根據該等高條形圖,完成下列![]() 列聯表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過0.05的前提下認為喜歡娛樂節目
列聯表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過0.05的前提下認為喜歡娛樂節目![]() 與觀眾性別有關?
與觀眾性別有關?

(2)從性觀眾中按喜歡節目![]() 與否,用分層抽樣的方法抽取5名做進一步調查.從這5名中任選2名,求恰有1名喜歡節目
與否,用分層抽樣的方法抽取5名做進一步調查.從這5名中任選2名,求恰有1名喜歡節目![]() 和1名不喜歡節目
和1名不喜歡節目![]() 的概率.
的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
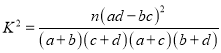 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐![]() 中,底面
中,底面![]() 是邊長為 2 的正三角形,頂點
是邊長為 2 的正三角形,頂點 ![]() 在底面
在底面![]() 上的射影為
上的射影為![]() 的中心,若
的中心,若![]() 為
為![]() 的中點,且直線
的中點,且直線![]() 與底面
與底面![]() 所成角的正切值為
所成角的正切值為![]() ,則三棱錐
,則三棱錐![]() 外接球的表面積為( )
外接球的表面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com