
已知冪函數(shù)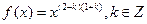 ,且
,且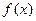 在
在 上單調(diào)遞增.
上單調(diào)遞增.
(Ⅰ)求實(shí)數(shù)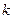 的值,并寫出相應(yīng)的函數(shù)
的值,并寫出相應(yīng)的函數(shù)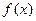 的解析式;
的解析式;
(II)若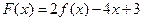 在區(qū)間
在區(qū)間 上不單調(diào),求實(shí)數(shù)
上不單調(diào),求實(shí)數(shù) 的取值范圍;
的取值范圍;
(III)試判斷是否存在正數(shù)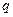 ,使函數(shù)
,使函數(shù)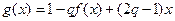 在區(qū)間
在區(qū)間 上的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/b0/9/1xu4r3.gif" style="vertical-align:middle;" />. 若存在,求出
上的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/b0/9/1xu4r3.gif" style="vertical-align:middle;" />. 若存在,求出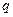 的值;若不存在,請說明理由
的值;若不存在,請說明理由
解:(Ⅰ)由題意知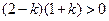 解得
解得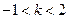
又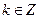 ∴
∴ 或
或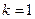 ,分別代入原函數(shù)得
,分別代入原函數(shù)得 .
.
(II)由已知得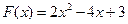 .
.
要使函數(shù)不單調(diào),則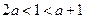 ,則
,則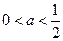 .
.
(III)由已知,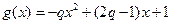
法一:假設(shè)存在這樣的正數(shù)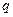 符合題意,則函數(shù)
符合題意,則函數(shù)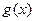 的圖象是開口向下的拋物線,其對稱軸為
的圖象是開口向下的拋物線,其對稱軸為
因而,函數(shù)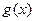 在
在 上的最小值只能在
上的最小值只能在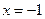 或
或 處取得
處取得
又 ,從而必有
,從而必有
解得
此時, ,其對稱軸
,其對稱軸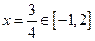
∴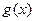 在
在 上的最大值為
上的最大值為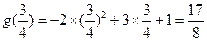 符合題意.
符合題意.
法二: 由(1)知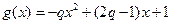 ,假設(shè)存在這樣的正數(shù)
,假設(shè)存在這樣的正數(shù)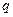 ,符合題意,則函數(shù)
,符合題意,則函數(shù)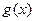
的圖象是開口向下的拋物線,其對稱軸為 ,
,
(1)當(dāng)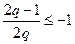 ,且
,且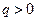 ,即
,即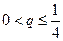 時,
時,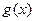 在
在 上單調(diào)遞減,
上單調(diào)遞減,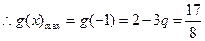 ,則
,則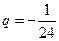 與
與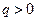 矛盾,故不可能;
矛盾,故不可能;
(2)當(dāng) ,且
,且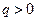 ,即
,即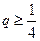 時,有
時,有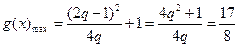
得 或
或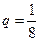 (舍去).
(舍去).
所以  ,此時
,此時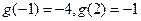 ,
,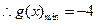 ,符合題意
,符合題意
綜上所述,存在正數(shù) ,使函數(shù)
,使函數(shù)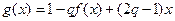 在區(qū)間
在區(qū)間 上的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/b0/9/1xu4r3.gif" style="vertical-align:middle;" />
上的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/b0/9/1xu4r3.gif" style="vertical-align:middle;" />
解析


 狀元坊全程突破導(dǎo)練測系列答案
狀元坊全程突破導(dǎo)練測系列答案 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 1 | 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
已知冪函數(shù)f(x)=x![]() (m∈Z)為偶函數(shù),且在區(qū)間(0,+∞)上是單調(diào)減函數(shù).
(m∈Z)為偶函數(shù),且在區(qū)間(0,+∞)上是單調(diào)減函數(shù).
(1)求函數(shù)f(x);
(2)討論F(x)=a![]() 的奇偶性.
的奇偶性.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年江西省吉安市白鷺洲中學(xué)高三(上)第一次月考數(shù)學(xué)試卷(文科)(解析版) 題型:解答題
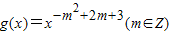 為偶函數(shù),且在區(qū)間(0,+∞)上是單調(diào)增函數(shù),又f(x)=sinx+mcosx,F(xiàn)(x)=f′(x)[f(x)+f′(x)]-1,f′(x)是f(x)的導(dǎo)函數(shù).
為偶函數(shù),且在區(qū)間(0,+∞)上是單調(diào)增函數(shù),又f(x)=sinx+mcosx,F(xiàn)(x)=f′(x)[f(x)+f′(x)]-1,f′(x)是f(x)的導(dǎo)函數(shù).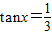 ,求F(x)的值;
,求F(x)的值;查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年廣東省高三8月月考文科數(shù)學(xué)試卷(解析版) 題型:解答題
已知冪函數(shù) 為偶函數(shù),且在區(qū)間
為偶函數(shù),且在區(qū)間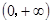 上是單調(diào)減函數(shù)(Ⅰ)求函數(shù)
上是單調(diào)減函數(shù)(Ⅰ)求函數(shù)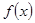 ;(Ⅱ)討論
;(Ⅱ)討論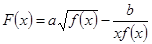 的奇偶性.
的奇偶性.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com