
| a | a+b |
|
| b |
| a |
| b |
| a |
| a |
| a+b |
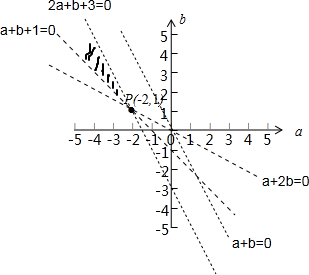 解:由程x2+(1+a)x+1+a+b=0的二次項系數為1>0,
解:由程x2+(1+a)x+1+a+b=0的二次項系數為1>0,
|
|
|
| a |
| a+b |
| 1 | ||
1+
|
| b |
| a |
| b-0 |
| a-0 |
|
| b |
| a |
| 1-0 |
| -2-0 |
| 1 |
| 2 |
| b |
| a |
| b |
| a |
| 1 |
| 2 |
| b |
| a |
| 1 | ||
1+
|
| b |
| a |
| 1 |
| 2 |
| 1 | ||
1+
|
| a |
| a+b |
|


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2a+3b |
| 3a |
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com