
已知函數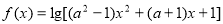 ,設命題
,設命題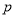 :“
:“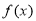 的定義域為
的定義域為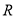 ”;
”;
命題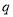 :“
:“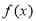 的值域為
的值域為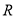 ” .
” .
(1)分別求命題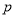 、
、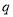 為真時實數
為真時實數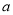 的取值范圍;
的取值范圍;
(2)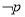 是
是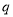 的什么條件?請說明理由.
的什么條件?請說明理由.
(1)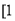 ,
,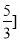 ;(2)
;(2) 是
是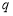 的必要而不充分的條件.
的必要而不充分的條件.
【解析】
試題分析:(1)命題p可轉化為恒成立問題,根據類二次函數的性質,可得到a的取值范圍;命題q可轉化為真數部分的值域包含(0,+∞),據些構造關于a的不等式組,解可得a的取值范圍;(2)由(1)求出?p,并比較兩個命題對應的參數a的范圍之間的包含關系,進而根據“誰小誰充分,誰大誰必要”可得答案.
試題解析:解:(1)命題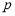 為真,即
為真,即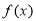 的定義域是
的定義域是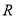 ,等價于
,等價于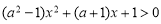 恒成立,
恒成立,
等價于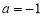 或
或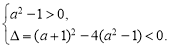
解得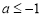 或
或 .∴實數
.∴實數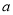 的取值范圍為
的取值范圍為 ,
,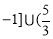 ,
,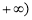
命題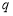 為真,即
為真,即 的值域是
的值域是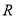 , 等價于
, 等價于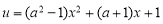 的值域
的值域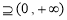 ,
,
等價于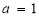 或
或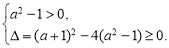
解得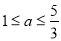 .∴實數
.∴實數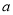 的取值范圍為
的取值范圍為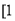 ,
,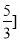
(2)由(1)(2)知, :
: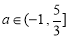 ;
;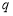 :
: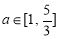 .
.
而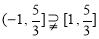 ,∴
,∴ 是
是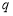 的必要而不充分的條件
的必要而不充分的條件
考點:1.必要條件、充分條件與充要條件的判斷;2.命題的真假判斷與應用.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com