【題目】已知三棱錐
中，側面
底面
，
，則三棱錐外接球的體積為（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】分析：由幾何關系首先求得外接球的半徑，然后利用球的體積公式求解體積的大小即可.
詳解：如圖取BC的中點為D，
顯然三棱錐P-ABC的外接球的球心O一定在過點D，且垂直于面ABC的垂線DO上.
設OD=h，在△PAC中，AC=4,PA=
,PC=
，
利用余弦定理得cos∠PCA=
.
在△PAC中過P作PH⊥AC，所以PH⊥平面ABC，易求PH=CH=1.
在△CDH中，CH=1，CD=
，
，
以DO與DH為鄰邊作矩形DOGH，
因為三棱錐P-ABC的外接球的球心為O，
所以OP=OB，OP2=(h+1)2+5,OB2=()2+h2，
那么
,解得OD=h=1，
可得外接球的半徑OB=3，
.
本題選擇B選項.
計算高手系列答案科目：高中數學 來源： 題型：
【題目】（2017高考新課標Ⅲ，理19）如圖，四面體ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．
（1）證明：平面ACD⊥平面ABC；
（2）過AC的平面交BD于點E，若平面AEC把四面體ABCD分成體積相等的兩部分，求二面角D–AE–C的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】 已知函數f(x)＝|x＋a|＋|x－2|.
(1)當a＝－3時，求不等式f(x)≥3的解集；
(2)若f(x)≤|x－4|的解集包含[1，2]，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)=loga(x+1)-loga(1-x),a>0且a≠1.
(1)求f(x)的定義域;
(2)判斷f(x)的奇偶性并予以證明;
(3)當a>1時,求使f(x)>0的解集.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】3名男生和3名女生共6人站成一排，若男生甲不站兩端，且不與男生乙相鄰，3名女生有且只有2名女生相鄰，則不同排法的種數是_____．（用數字作答）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】業界稱“中國芯”迎來發展和投資元年，某芯片企業準備研發一款產品，研發啟動時投入資金為
(為常數)元,之后每年會投入一筆研發資金,
年后總投入資金記為
,經計算發現當
時,近似地滿足
，其中
為常數,
.已知
年后總投入資金為研發啟動時投入資金的倍．問
（1）研發啟動多少年后,總投入資金是研發啟動時投入資金的
倍;
（2）研發啟動后第幾年的投入資金的最多.
查看答案和解析>>
科目：高中數學 來源： 題型：
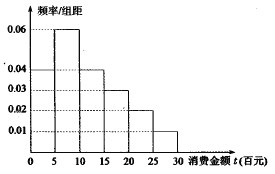
【題目】“雙十一”已經成為網民們的網購狂歡節，某電子商務平臺對某市的網民在今年“雙十一”的網購情況進行摸底調查，用隨機抽樣的方法抽取了100人，其消費金額
(百元)的頻率分布直方圖如圖所示：
(1)求網民消費金額
的平均值和中位數
；
(2)把下表中空格里的數填上，能否有
的把握認為網購消費與性別有關；
男 | 女 | 合計 | |
| |||
| 30 | ||
合計 | 45 |
附表：
|
|
|
|
|
|
|
|
.
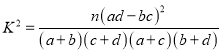查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
過點
，且兩個焦點的坐標分別為
， 
.
（1）求
的方程；
（2）若
， 
， 
為
上的三個不同的點， 
為坐標原點，且
，求證：四邊形
的面積為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
