
在等腰梯形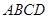 中,
中,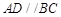 ,
,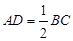 ,
,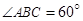 ,
,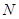 是
是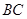 的中點(diǎn).將梯形
的中點(diǎn).將梯形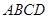 繞
繞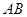 旋轉(zhuǎn)
旋轉(zhuǎn)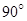 ,得到梯形
,得到梯形 (如圖).
(如圖).

(1)求證: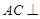 平面
平面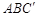 ;
;
(2)求證: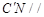 平面
平面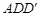 ;
;
(3)求二面角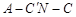 的余弦值.
的余弦值.
(1)根據(jù)題意,由于即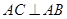 由已知可知 平面
由已知可知 平面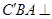 平面
平面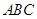 ,結(jié)合面面垂直的性質(zhì)定理得到.
,結(jié)合面面垂直的性質(zhì)定理得到.
(2)結(jié)合題意,得到面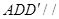 平面
平面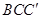 ,又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013081212195008027017/SYS201308121220203508453943_DA.files/image006.png">平面
,又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013081212195008027017/SYS201308121220203508453943_DA.files/image006.png">平面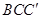 ,所以
,所以
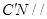 平面
平面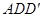 從而得到證明.
從而得到證明.
(3) 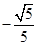
【解析】
試題分析:(1)證明:因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013081212195008027017/SYS201308121220203508453943_DA.files/image010.png">,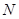 是
是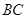 的中點(diǎn)
的中點(diǎn)
所以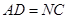 ,又
,又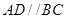
所以四邊形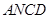 是平行四邊形,所以
是平行四邊形,所以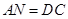
又因?yàn)榈妊菪危?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013081212195008027017/SYS201308121220203508453943_DA.files/image017.png">,
所以 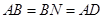 ,所以四邊形
,所以四邊形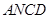 是菱形,所以
是菱形,所以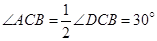

所以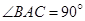 ,即
,即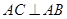
由已知可知 平面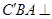 平面
平面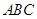 ,
,
因?yàn)?平面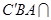 平面
平面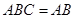
所以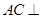 平面
平面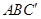 4分
4分
(2)證明:因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013081212195008027017/SYS201308121220203508453943_DA.files/image014.png">,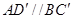 ,
,
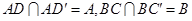
所以平面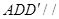 平面
平面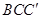
又因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013081212195008027017/SYS201308121220203508453943_DA.files/image006.png">平面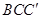 ,所以
,所以
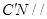 平面
平面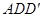 8分
8分
(3)因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013081212195008027017/SYS201308121220203508453943_DA.files/image024.png">平面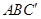 ,同理
,同理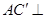 平面
平面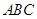 ,建立如圖如示坐標(biāo)系
,建立如圖如示坐標(biāo)系
設(shè) ,
,
則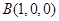 ,
,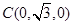 ,
, 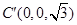 ,
,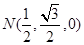 ,
9分
,
9分
則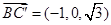 ,
,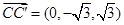
設(shè)平面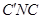 的法向量為
的法向量為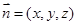 ,有
,有 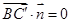 ,
,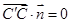 得
得 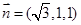
設(shè)平面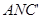 的法向量為
的法向量為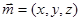 ,有
,有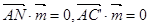
得
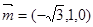 12分
12分
所以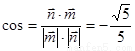 13分
13分
由圖形可知二面角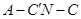 為鈍角
為鈍角
所以二面角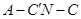 的余弦值為
的余弦值為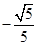 .
14分
.
14分
考點(diǎn):平行和垂直的證明以及二面角的平面角
點(diǎn)評:主要是考查了線面平行以及面面平行的性質(zhì)定理的運(yùn)用,以及二面角的求解,屬于基礎(chǔ)題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
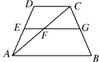 如圖,在等腰梯形中,AB∥CD,AD=12 cm,AC交梯形中位線EG于點(diǎn)F,EF=4cm,
如圖,在等腰梯形中,AB∥CD,AD=12 cm,AC交梯形中位線EG于點(diǎn)F,EF=4cm,查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年浙江省高三第一學(xué)期八校聯(lián)考理科數(shù)學(xué) 題型:解答題
(本題滿分15分) 如圖所示,在等腰梯形 中,
中, ,
, ,
, 為
為 中點(diǎn).將
中點(diǎn).將 沿
沿 折起至
折起至 ,使得平面
,使得平面 平面
平面 ,
, 分別為
分別為 的中點(diǎn).
的中點(diǎn).
(Ⅰ) 求證: 面
面 ;
;
(Ⅱ) 求二面角 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年江蘇省高三下學(xué)期期末考試數(shù)學(xué)試卷 題型:填空題
在等腰梯形 中,
中, ,且
,且 。設(shè)以
。設(shè)以 為焦點(diǎn)且過點(diǎn)
為焦點(diǎn)且過點(diǎn) 的雙曲線的離心率為
的雙曲線的離心率為 ,以
,以 為焦點(diǎn)且過點(diǎn)
為焦點(diǎn)且過點(diǎn) 的橢圓的離心率為
的橢圓的離心率為 ,則
,則 = ;
= ;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年黑龍江省高二上學(xué)期期中考試數(shù)學(xué)理卷 題型:選擇題
如圖,在等腰梯形 中,
中, ,且
,且 .設(shè)
.設(shè) ,以
,以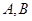 為焦點(diǎn)且過點(diǎn)
為焦點(diǎn)且過點(diǎn) 的雙曲線的離心率為
的雙曲線的離心率為 ,以
,以 為焦點(diǎn)且過點(diǎn)
為焦點(diǎn)且過點(diǎn) 的橢圓的離心率為
的橢圓的離心率為 ,則
( )
,則
( )
A.隨著角度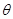 的增大,
的增大, 增大,
增大, 為定值
為定值
B.隨著角度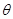 的增大,
的增大, 減小,
減小, 為定值
為定值
C.隨著角度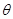 的增大,
的增大, 增大,
增大, 也增
也增
D.隨著角度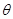 的增大,
的增大, 減小,
減小, 也減小
也減小

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com