
如圖,在矩形ABCD中,AB=4,AD=2,E為AB的中點,現將△ ADE沿直線DE翻折成△A′DE,使平面A′DE⊥平面BCDE,F為線段A′D的中點.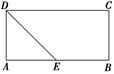
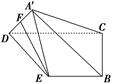
(1)求證:EF//平面A′BC;
(2)求直線A′B與平面A′DE所成角的正切值.
(1)要證明線面平行,只要通過證明線線平行來得到即可。
(2)
解析試題分析:解:(1)證明:取A′C的中點M,連結MF,MB,則FM∥DC,且FM= DC.
DC.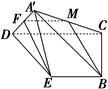
∵EB∥DC,且EB= DC,
DC,
∴FM∥EB且FM=EB.
∴四邊形EBMF為平行四邊形,
∴EF∥MB.
∵EF 平面A′BC,MB
平面A′BC,MB 平面A′BC,
平面A′BC,
∴EF∥平面A′BC. 4分
(2)過B作BO垂直于DE的延長線,O為垂足,連結A′O.
∵平面A′DE⊥平面BCDE,且平面A′DE∩平面BCDE=DE,
∴BO⊥平面A′DE,
∴∠BA′O就是直線A′B與平面A′DE所成的角. 7分
過A′作A′S⊥DE,S為垂足,
因為平面A′DE⊥平面BCDE,且平面A′DE∩平面BCDE=DE,
所以A′S⊥平面BCDE.
在Rt△A′SO中,A′S= ,SO=2
,SO=2 ,所以A′O=
,所以A′O=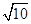 .
.
又BO= ,所以tan∠BA′O=
,所以tan∠BA′O=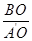 =
= =
= ,
,
故直線A′B與平面A′DE所成角的正切值為 . 10分
. 10分
考點:直線與平面平行的判定定理
點評:本題主要考查了直線與平面平行的判定定理與線面平行與線線平行的相互轉化,還考查了直線與平面所成角的求解,要注意利用已知圖形構造直角三角形進行求解.


科目:高中數學 來源: 題型:解答題
如圖(1),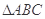 是等腰直角三角形,其中
是等腰直角三角形,其中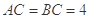 ,
,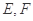 分別為
分別為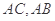 的中點,將
的中點,將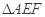 沿
沿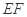 折起,點
折起,點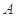 的位置變為點
的位置變為點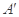 ,已知點
,已知點 在平面
在平面 上的射影
上的射影 為
為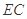 的中點,如圖(2)所示.
的中點,如圖(2)所示.
(1)求證: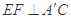 ;
;
(2)求三棱錐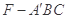 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
AB為圓O的直徑,點E、F在圓上,AB//EF,矩形ABCD所在平面與圓O所在平面互相垂直,已知AB=2,BC=EF=1。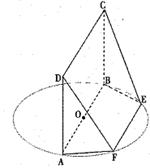
(I)求證:BF⊥平面DAF;
(II)求ABCD與平面CDEF所成銳二面角的某三角函數值;
(III)求多面體ABCDFE的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
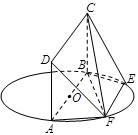
如圖,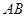 為圓
為圓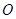 的直徑,點
的直徑,點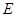 、
、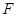 在圓
在圓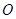 上,
上,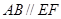 ,矩形
,矩形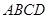 所在的平面與圓
所在的平面與圓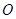 所在的平面互相垂直.已知
所在的平面互相垂直.已知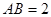 ,
,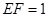 .
.
(Ⅰ)求證:平面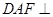 平面
平面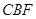 ;
;
(Ⅱ)求直線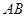 與平面
與平面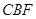 所成角的大小;
所成角的大小;
(Ⅲ)當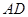 的長為何值時,平面
的長為何值時,平面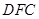 與平面
與平面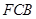 所成的銳二面角的大小為
所成的銳二面角的大小為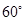 ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
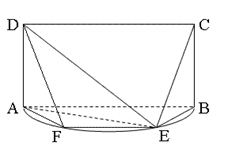
如圖, 是以
是以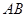 為直徑的半圓上異于
為直徑的半圓上異于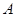 、
、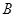 的點,矩形
的點,矩形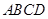 所在的平面垂直于該半圓所在的平面,且
所在的平面垂直于該半圓所在的平面,且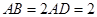 .
.
(Ⅰ)求證: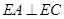 ;
;
(Ⅱ)設平面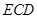 與半圓弧的另一個交點為
與半圓弧的另一個交點為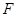 .
.
①試證: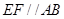 ;
;
②若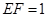 ,求三棱錐
,求三棱錐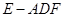 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,正方體ABCD—A1B1C1D1中,E為AB中點,F為正方形BCC1B1的中心.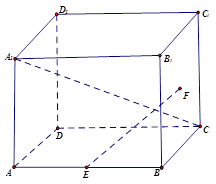
(1)求直線EF與平面ABCD所成角的正切值;
(2)求異面直線A1C與EF所成角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com