Question

已知兩條直線m，n，兩個平面α，β．下面四個命題中不正確的是（ ）
A．m∥n，m⊥α⇒n⊥α
B．α∥β，m∥n，m⊥α⇒n⊥β
C．m∥n，m∥α⇒n∥α
D．α⊥β⊥γ，α∩β=n⇒n⊥γ

Answer 1

【答案】分析：A．利用結論“兩條平行線中的一條垂直于平面，則另一條也垂直于這個平面”即可判斷；
B．同上；
C．可能有n?α，因此不全面；
D．如圖所示，可利用線面、面面垂直的判定和性質定理證明正確．
解答：解：A．根據“兩條平行線中的一條垂直于平面，則另一條也垂直于這個平面”，得m∥n，m⊥α⇒n⊥α，正確；
B．根據同上，正確；
C．由m∥n，m∥α，可得n∥α或n?α，故不正確；
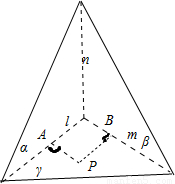
D．如圖所示：設α∩γ=l，β∩γ=m，取點P∈γ，過點P作PA⊥l，PB⊥m，垂足分別為A、B，
∵α⊥γ，β⊥γ，∴PA⊥α，PB⊥β，
又∵α∩β=n，∴PA⊥n，PB⊥n，∴n⊥γ，故正確．
綜上可知：不正確的是C．
故選C．
點評：熟練正確線線、線面、面面的平行與垂直的性質與判定定理是解題的關鍵．