
【題目】網購是當前民眾購物的新方式,某公司為改進營銷方式,隨機調查了100名市民,統計其周平均網購的次數,并整理得到如下的頻數分布直方圖.這100名市民中,年齡不超過40歲的有65人將所抽樣本中周平均網購次數不小于4次的市民稱為網購迷,且已知其中有5名市民的年齡超過40歲.
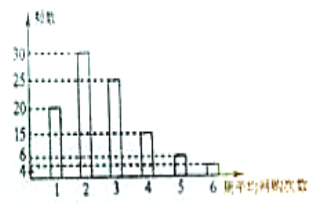
(1)根據已知條件完成下面的![]() 列聯表,能否在犯錯誤的概率不超過0.10的前提下認為網購迷與年齡不超過40歲有關?
列聯表,能否在犯錯誤的概率不超過0.10的前提下認為網購迷與年齡不超過40歲有關?
網購迷 | 非網購迷 | 合計 | |
年齡不超過40歲 | |||
年齡超過40歲 | |||
合計 |
(2)若從網購迷中任意選取2名,求其中年齡超過40歲的市民人數![]() 的分布列與期望.
的分布列與期望.
附: 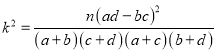 ;
;
| 0.15 | 0.10 | 0.05 | 0.01 |
| 2.072 | 2.706 | 3.841 | 6.635 |
【答案】(1)詳見解析;(2)詳見解析.
【解析】試題分析:
(1)利用題意繪制列聯表即可,求得![]()
![]() .所以可以在犯錯誤的概率不超過0.10的前提下認為網購迷與年齡不超過40歲有關;
.所以可以在犯錯誤的概率不超過0.10的前提下認為網購迷與年齡不超過40歲有關;
(2)該分布列為超幾何分布,寫出分布列可得![]() .
.
試題解析:
(1)由題意可得列聯表如下:
網購迷 | 非網購迷 | 合計 | |
年齡不超過40歲 | 20 | 45 | 65 |
年齡超過40歲 | 5 | 30 | 35 |
合計 | 25 | 75 | 100 |
假設網購迷與年齡不超過40歲沒有關系,
則![]()
![]() .
.
所以可以在犯錯誤的概率不超過0.10的前提下認為網購迷與年齡不超過40歲有關;
(2)由頻率分布直方圖可知,網購迷共有25名,由題意得年齡超過40的市民人數![]() 的所有取值為0,1,2,
的所有取值為0,1,2,
![]() ,
, ![]() ,
, ![]() ,
,
![]()
![]() 的分布列為
的分布列為
| 0 | 1 | 2 |
|
|
|
|
![]()
![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)的定義域為R,且f(x)不為常值函數,有以下命題:
①函數g(x)=f(x)+f(﹣x)一定是偶函數;
②若對任意x∈R都有f(x)+f(2﹣x)=0,則f(x)是以2為周期的周期函數;
③若f(x)是奇函數,且對于任意x∈R,都有f(x)+f(2+x)=0,則f(x)的圖象的對稱軸方程為x=2n+1(n∈Z);
④對于任意的x1 , x2∈R,且x1≠x2 , 若![]() >0恒成立,則f(x)為R上的增函數,
>0恒成立,則f(x)為R上的增函數,
其中所有正確命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有若干(大于20)件某種自然生長的中藥材,從中隨機抽取20件,其重量都精確到克,規定每件中藥材重量不小于15克為優質品.如圖所示的程序框圖表示統計20個樣本中的優質品數,其中![]() 表示每件藥材的重量,則圖中①,②兩處依次應該填的整數分別是____________.
表示每件藥材的重量,則圖中①,②兩處依次應該填的整數分別是____________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某青少年成長關愛機構為了調研所在地區青少年的年齡與身高壯況,隨機抽取6歲,9歲,12歲,15歲,18歲的青少年身高數據各1000個,根據各年齡段平均身高作出如圖所示的散點圖和回歸直線![]() .根據圖中數據,下列對該樣本描述錯誤的是( )
.根據圖中數據,下列對該樣本描述錯誤的是( )
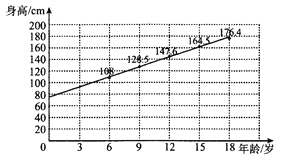
A. 據樣本數據估計,該地區青少年身高與年齡成正相關
B. 所抽取數據中,5000名青少年平均身高約為![]()
C. 直線![]() 的斜率的值近似等于樣本中青少年平均身高每年的增量
的斜率的值近似等于樣本中青少年平均身高每年的增量
D. 從這5種年齡的青少年中各取一人的身高數據,由這5人的平均年齡和平均身高數據作出的點一定在直線![]() 上
上
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙曲線 ![]() =1(a>0,b>0)的左右焦點分別為F1 , F2漸近線分別為l1 , l2 , 位于第一象限的點P在l1上,若l2⊥PF1 , l2∥PF2 , 則雙曲線的離心率是( )
=1(a>0,b>0)的左右焦點分別為F1 , F2漸近線分別為l1 , l2 , 位于第一象限的點P在l1上,若l2⊥PF1 , l2∥PF2 , 則雙曲線的離心率是( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】集合A={(x,y)|y=a},集合B={(x,y)|y=bx+1,b>0,b≠1},若集合A∩B≠,則實數a的取值范圍是( )
A.(﹣∞,1)
B.(﹣∞,1]
C.[1,+∞)
D.(1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,D是BC的中點. 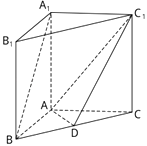
(1)求證:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求幾何體ABD﹣A1B1C1的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com