
(江西卷理22)已知函數(shù)![]() ,
,![]() .
.
![]() .當(dāng)
.當(dāng)![]() 時,求
時,求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
![]() .對任意正數(shù)
.對任意正數(shù)![]() ,證明:
,證明:![]() .
.
【試題解析】
![]() 、當(dāng)
、當(dāng)![]() 時,
時,![]() ,求得
,求得  ,
,
于是當(dāng)![]() 時,
時,![]() ;而當(dāng)
;而當(dāng) ![]() 時,
時,![]() .
.
即![]() 在
在![]() 中單調(diào)遞增,而在
中單調(diào)遞增,而在![]() 中單調(diào)遞減.
中單調(diào)遞減.
(2).對任意給定的![]() ,
,![]() ,由
,由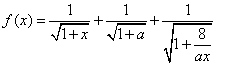 ,
,
若令 ![]() ,則
,則 ![]() … ① ,而
… ① ,而 ![]() … ②
… ②
(一)、先證![]() ;因為
;因為![]() ,
,![]() ,
,![]() ,
,
又由 ![]() ,得
,得 ![]() .
.
所以![]()
![]()
![]()
![]() .
.
(二)、再證![]() ;由①、②式中關(guān)于
;由①、②式中關(guān)于![]() 的對稱性,不妨設(shè)
的對稱性,不妨設(shè)![]() .則
.則![]()
(ⅰ)、當(dāng)![]() ,則
,則![]() ,所以
,所以![]() ,因為
,因為 ![]() ,
,
![]() ,此時
,此時![]() .
.
(ⅱ)、當(dāng)![]() …③,由①得 ,
…③,由①得 ,![]() ,
,![]() ,
,
因為 ![]() 所以
所以 ![]() … ④
… ④
同理得![]() … ⑤ ,于是
… ⑤ ,于是  … ⑥
… ⑥
今證明 ![]() … ⑦, 因為
… ⑦, 因為 ![]() ,
,
只要證 ![]() ,即
,即 ![]() ,也即
,也即 ![]() ,據(jù)③,此為顯然.
,據(jù)③,此為顯然.
因此⑦得證.故由⑥得 ![]() .
.
綜上所述,對任何正數(shù)![]() ,皆有
,皆有![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
(江西卷理22)已知函數(shù)![]() ,
,![]() .
.
![]() .當(dāng)
.當(dāng)![]() 時,求
時,求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
![]() .對任意正數(shù)
.對任意正數(shù)![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (江西卷理20文22)如圖,正三棱錐
(江西卷理20文22)如圖,正三棱錐![]() 的三條側(cè)棱
的三條側(cè)棱![]() 、
、![]() 、
、![]() 兩兩垂直,且長度均為2.
兩兩垂直,且長度均為2.![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,
的中點,![]() 是
是![]() 的中點,過
的中點,過![]() 作平面與側(cè)棱
作平面與側(cè)棱![]() 、
、![]() 、
、![]() 或其延長線分別相交于
或其延長線分別相交于![]() 、
、![]() 、
、![]() ,已知
,已知![]() .
.
(1).求證:![]() ⊥平面
⊥平面![]() ;
;
(2).求二面角![]() 的大小;
的大小;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (江西卷理20文22)如圖,正三棱錐
(江西卷理20文22)如圖,正三棱錐![]() 的三條側(cè)棱
的三條側(cè)棱![]() 、
、![]() 、
、![]() 兩兩垂直,且長度均為2.
兩兩垂直,且長度均為2.![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,
的中點,![]() 是
是![]() 的中點,過
的中點,過![]() 作平面與側(cè)棱
作平面與側(cè)棱![]() 、
、![]() 、
、![]() 或其延長線分別相交于
或其延長線分別相交于![]() 、
、![]() 、
、![]() ,已知
,已知![]() .
.
(1).求證:![]() ⊥平面
⊥平面![]() ;
;
(2).求二面角![]() 的大小;
的大小;
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com