Question

設(shè)數(shù)列{}的前n項和為，并且滿足，（n∈N*）.

（Ⅰ）求，，；（Ⅱ）猜想{}的通項公式，并加以證明；　

（Ⅲ）設(shè)，，且，證明：≤.

Answer 1

解：（Ⅰ）分別令，2，3，得

　　　 ∵，

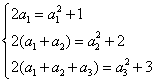
∴，，　　　 …………………3分

　 （Ⅱ）證法一：

猜想：，　　　　　　 ……………………4分

　　　　　　 由　 　　　　　　　　①

　　　 可知，當(dāng)≥2時，

②　　　　　 ①－②，得 ，

即.　　 ………………6分

　　　1）當(dāng)時，

，

∵，

∴；　　　　　 ……………7分

　　　 2）假設(shè)當(dāng)（≥2）時，.

那么當(dāng)時，

　　　　　　 ，

∵，≥2，

∴，

　　　　　 ∴.　　　　

這就是說，當(dāng)時也成立，

　　　　 ∴（≥2）.

顯然時，也適合.

　　　　 故對于n∈N*，均有.　　　 ……………………9分

　　 證法二：猜想：，　　　　 ……………………………4分

　　 1）當(dāng)時，成立；　　　 ……………………………5分

　　 2）假設(shè)當(dāng)時，.　　　 …………………………6分

　　　 那么當(dāng)時，.

∴，　　　　　 ∴

　　　　　 （以下同證法一） ………………9分

（Ⅲ）證法一：要證≤，

只要證≤，…………10分

　　 即≤，…………11分

將代入，得≤，

即要證≤，

即≤1. …………………………12分

∵，，且，

∴≤,

即≤，故≤1成立，

所以原不等式成立. ………………………14分

證法二：∵，，且，

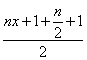∴≤　　 ①

當(dāng)且僅當(dāng)時取“”號. 　………………………11分

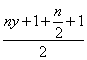∴≤　　 ②

當(dāng)且僅當(dāng)時取“”號. 　……………………12分

①+②，

得（）≤，

當(dāng)且僅當(dāng)時取“”號.　　 ………………………13分

∴≤.　 ……………………14分　

　 證法三：可先證≤.　 　 ……………………10分

　　　　　 ∵，

　　　　　 ，

≥，……………………………11分

　　　　　 ∴≥，

∴≥，

當(dāng)且僅當(dāng)時取等號. ………………12分

　　　　 令，，

即得：≤，

　　　　 當(dāng)且僅當(dāng)

即時取等號. ………………………14分