
(2007
北京,16)如下圖,在Rt△AOB中,∠OAB=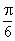 ,斜邊AB=4,Rt△AOC可以通過Rt△AOB以直線AO為軸旋轉得到,且二面角B-AO-C是直二面角.動點D在斜邊AB上.
,斜邊AB=4,Rt△AOC可以通過Rt△AOB以直線AO為軸旋轉得到,且二面角B-AO-C是直二面角.動點D在斜邊AB上.
(1)
求證:平面COD⊥平面AOB;(2)
當D為AB的中點時,求異面直線AO與CD所成角的大小;(3)
求CD與平面AOB所成角的最大值.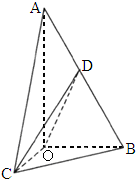
|
解析: (1)由題意,CO⊥AO,BO⊥AO,∴∠ BOC是二面角B-AO-C的平面角.又∵二面角 B-AO-C是直二面角,∴CO⊥BO,又∵AO∩BO=0,∴ CO⊥平面AOB,又 CO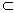 平面COD, 平面COD,
∴平面 COD⊥平面AOB.(2) 作DE⊥OB,垂足為E,連結CE(如下圖),則DE∥AO,∴∠CDE是異面直線AO與CD所成的角.
在 Rt△COE中,CO=BO=2,OE=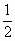 BO=1,∴CE= BO=1,∴CE=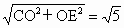 . .
又 DE=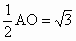 ,∴在Rt△CDE中,tan∠CDE= ,∴在Rt△CDE中,tan∠CDE=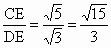 , ,
∴異面直線 AO與CD所成角的大小為 . .
(3) 由(1)知,CO⊥平面AOB,∴∠ CDO是CD與平面AOB所成的角,且 tan∠CDO=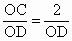 .當OD最小時,∠CDO最大,這時,OD⊥AB,垂足為D, .當OD最小時,∠CDO最大,這時,OD⊥AB,垂足為D,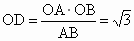 , ,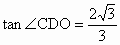 , ,
∴ CD與平面AOB所成角的最大值為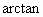 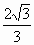 . . |
|
剖析:本題考查立體幾何的旋轉問題和異面直線所成的角,以及空間想象能力和邏輯推理能力. |


科目:高中數學 來源: 題型:013
(2007
北京西城模擬)在1,2,3,4,5這五個數字所組成的沒有重復數字的三位數中,其各個數字之和為9的三位數共有[
]|
A .16個 |
B .18個 |
C .19個 |
D .21個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com