
【題目】已知長方體![]() 中,
中, ![]() 為
為![]() 的中點,
的中點, ![]() 在棱
在棱![]() 上,
上, ![]() ,
, ![]() .
.
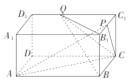
(1)若異面直線![]() 與
與![]() 互相垂直,求
互相垂直,求![]() 的長;
的長;
(2)當四棱錐![]() 的體積為
的體積為![]() 時,求證:直線
時,求證:直線![]() 平面
平面![]() .
.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:如圖,以![]() 為原點,分別以
為原點,分別以![]() 所在的直線為
所在的直線為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立空間直角坐標系.得到相應點和相應向量的坐標,利用空間向量的夾角公式可得
軸建立空間直角坐標系.得到相應點和相應向量的坐標,利用空間向量的夾角公式可得![]() 的長
的長
(2)證明:因為![]() 是長方體,
是長方體, ![]() 在棱
在棱![]() 上,所以
上,所以![]() 平面
平面![]() ,
,
所以四棱錐![]() 的體積
的體積![]() ,解得
,解得![]() .
.
此時![]() 為
為![]() 的中點,所以
的中點,所以![]() . 利用空間向量的知識可證得直線
. 利用空間向量的知識可證得直線![]() 平面
平面![]() ..
..
試題解析:(1)如圖,以![]() 為原點,分別以
為原點,分別以![]() 所在的直線為
所在的直線為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立空間直角坐標系.
軸建立空間直角坐標系.
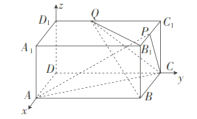
則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
設![]() ,則
,則![]() ,
, ![]() ,
,
因為![]() ,所以
,所以![]() ,即
,即![]() ,解得
,解得![]() .
.
所以,當異面直線![]() 與
與![]() 互相垂直時,
互相垂直時, ![]() .
.
(2)證明:因為![]() 是長方體,
是長方體, ![]() 在棱
在棱![]() 上,所以
上,所以![]() 平面
平面![]() ,
,
所以四棱錐![]() 的體積
的體積![]()
![]() ,解得
,解得![]() .
.
此時![]() 為
為![]() 的中點,所以
的中點,所以![]() .
.
由(1)可知![]() ,
, ![]() ,
, ![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,則
,則 ,即
,即![]() ,
,
令![]() ,得
,得![]() ,
, ![]() ,所以
,所以![]() ,
,
因為![]() ,
,
所以![]() ,因為直線
,因為直線![]() 平面
平面![]() ,
,
所以直線![]() 平面
平面![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左焦點為
的左焦點為![]() ,過點
,過點![]() 做
做![]() 軸的垂線交橢圓于
軸的垂線交橢圓于![]() 兩點,且
兩點,且![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 為橢圓
為橢圓![]() 短軸的上頂點,直線
短軸的上頂點,直線![]() 不經過
不經過![]() 點且與
點且與![]() 相交于
相交于![]() 兩點,若直線
兩點,若直線![]() 與直線
與直線![]() 的斜率的和為
的斜率的和為![]() ,問:直線
,問:直線![]() 是否過定點?若是,求出這個定點,否則說明理由.
是否過定點?若是,求出這個定點,否則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() :
: ![]()
![]() 的焦距與橢圓
的焦距與橢圓![]() :
: ![]() 的短軸長相等,且
的短軸長相等,且![]() 與
與![]() 的長軸長相等,這兩個橢圓在第一象限的交點為
的長軸長相等,這兩個橢圓在第一象限的交點為![]() ,直線
,直線![]() 經過
經過![]() 在
在![]() 軸正半軸上的頂點
軸正半軸上的頂點![]() 且與直線
且與直線![]() (
(![]() 為坐標原點)垂直,
為坐標原點)垂直, ![]() 與
與![]() 的另一個交點為
的另一個交點為![]() ,
, ![]() 與
與![]() 交于
交于![]() ,
, ![]() 兩點.
兩點.
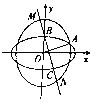
(1)求![]() 的標準方程;
的標準方程;
(2)求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2-2ax-1+a,a∈R.
(1)若a=2,試求函數y=![]() (x>0)的最小值;
(x>0)的最小值;
(2)對于任意的x∈[0,2],不等式f(x)≤a成立,試求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設關于某設備的使用年限![]() (年)和所支出的維修費用
(年)和所支出的維修費用![]() (萬元)有如下統計資料:
(萬元)有如下統計資料:
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由資料知, ![]() 對
對![]() 呈線性相關關系,試求:
呈線性相關關系,試求:
(1)回歸直線方程;
(2)估計使用年限為10年時,維修費用約是多少?
參考公式:回歸直線方程: ![]() .其中
.其中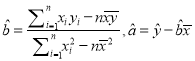
(注: ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】右圖是一個幾何體的平面展開圖,其中ABCD為
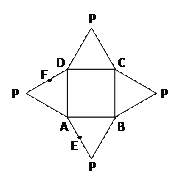
正方形, E、F分別為PA、PD的中點,在此幾何體中,
給出下面四個結論:
①直線BE與直線CF異面;②直線BE與直線AF異面;
③直線EF//平面PBC; ④平面BCE⊥平面PAD.
其中正確結論的個數是
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com