已知向量
＝(2cosα,2sinα), 
＝(3cosβ,3sinβ),若與的夾角為60°,則直線
與圓
的位置關系是( )
A.相交 B.相交且過圓心 C.相切 D.相離
D
【解析】
試題分析：∵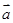
＝(2cosα,2sinα), 
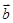＝(3cosβ,3sinβ),
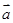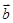∴||＝2,| |＝3.
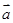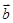∴·＝6cosαcosβ+6sinαsinβ＝6cos(α-β).
而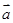·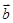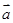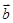＝||||cos60°＝3,
∴6cos(α-β)＝3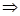
cos(α-β)＝
.
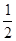則圓心(cosβ,-sinβ)到直線xcosα-ysinα+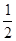＝0的距離d＝|cosαcosβ+sinαsinβ+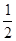|＝|cos(α-β)+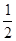|＝1＞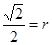
,∴相離.故選D。
考點：本題主要考查平面向量的坐標運算及數量積應用。
點評：判斷直線與圓的位置關系，常常用幾何法，即研究圓心到直線的距離與半徑比較大小。向量及數量積符號表示要規范。綜合性較強的題目。
高中必刷題系列答案科目：高中數學 來源：吉林省東北師大附中2009－2010學年高一上學期期末考試數學試題 題型：044
已知向量
＝(cosx，1－asinx)，
＝(cosx，2)，其中a∈R，x∈R，設f(x)＝·，且函數f(x)的最大值為g(a)．
(Ⅰ)求函數g(a)的解析式；
(Ⅱ)設0≤
≤2π，求函數g(2cos＋1)的最大值和最小值以及對應的值；
(Ⅲ)若對于任意的實數x∈R，g(x)≥kx＋
恒成立，求實數k的取值范圍．
查看答案和解析>>
科目：高中數學 來源：浙江省臺州中學2012屆高三上學期期中考試數學理科試題 題型：022
已知向量
＝(2cosα，2sinα)，
＝(2cosβ，2sinβ)，且直線2xcosα－2ysinα＋1＝0與圓(x－cosβ)2＋(y＋sinβ)2＝1相切，則向量與的夾角為________．
查看答案和解析>>
科目：高中數學 來源：重慶市西南師大附中2010屆高三下學期3月月考數學理科試題 題型：044
已知向量
＝(2cosωx，1)，
＝(sinωx＋cosωx，－1)，(ω∈R，ω＞0)，設函數f(x)＝
(x∈R)，若f(x)的最小正周期為
．
(1)求ω的值；
(2)求f(x)的單調區間．
查看答案和解析>>
科目：高中數學 來源：重慶市西南師大附中2010屆高三下學期3月月考數學文科試題 題型：044
已知向量
＝(2cosωx，1)，
＝(sinωx＋cosωx，－1)，(ω∈R，ω＞0)，設函數f(x)＝
(x∈R)，若f(x)的最小正周期為
．
(1)求ω的值；
(2)求f(x)的單調區間．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com