
【題目】某種藥種植基地有兩處種植區的藥材需在下周一、周二兩天內采摘完畢,基地員工一天可以完成一處種植區的采摘,由于下雨會影響藥材的收益,若基地收益如下表所示:已知下周一和下周二無雨的概率相同且為![]() ,兩天是否下雨互不影響,若兩天都下雨的概率為
,兩天是否下雨互不影響,若兩天都下雨的概率為![]()

(1)求![]() 及基地的預期收益;
及基地的預期收益;
(2)若該基地額外聘請工人,可在周一當天完成全部采摘任務,若周一無雨時收益為![]() 萬元,有雨時收益為
萬元,有雨時收益為![]() 萬元,且額外聘請工人的成本為
萬元,且額外聘請工人的成本為![]() 元,問該基地是否應該額外聘請工人,請說明理由.
元,問該基地是否應該額外聘請工人,請說明理由.
【答案】(1) ![]() 基地的預期收益為9.16萬元;(2)見解析.
基地的預期收益為9.16萬元;(2)見解析.
【解析】試題分析:
(1)由于兩天下雨是相互獨立的,因此兩天都下雨的概率是![]() ,由此可得
,由此可得![]() ;該基地收益
;該基地收益![]() 的可能取值為10,8, 5(單位:萬元),分別計算要概率,然后列出概率分布列,計算出數學期望.(2)該基地額外聘請工人的預期收益絕對值計算易得,現第(1)小題,比較兩個預期值可得.
的可能取值為10,8, 5(單位:萬元),分別計算要概率,然后列出概率分布列,計算出數學期望.(2)該基地額外聘請工人的預期收益絕對值計算易得,現第(1)小題,比較兩個預期值可得.
試題解析:
(1) 兩天都下雨的概率為![]() ,解得
,解得![]() .
.
該基地收益![]() 的可能取值為10,8, 5。(單位:萬元)則:
的可能取值為10,8, 5。(單位:萬元)則:
![]() ,
, ![]() ,
, ![]()
所以該基地收益![]() 的分布列為:
的分布列為:
| 10 | 8 | 5 |
| 0.64 | 0.32 | 0.04 |
則該基地的預期收益![]() (萬元)
(萬元)
所以,基地的預期收益為9.16萬元
⑵設基地額外聘請工人時的收益為![]() 萬元,則其預期收益:
萬元,則其預期收益:
![]() (萬元)
(萬元)
此時![]() ,所以該基地應該外聘工人.
,所以該基地應該外聘工人.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:高中數學 來源: 題型:
【題目】已知圓![]() :
: ![]() 過橢圓
過橢圓![]() :
: ![]() (
(![]() )的短軸端點,
)的短軸端點, ![]() ,
, ![]() 分別是圓
分別是圓![]() 與橢圓
與橢圓![]() 上任意兩點,且線段
上任意兩點,且線段![]() 長度的最大值為3.
長度的最大值為3.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過點![]() 作圓
作圓![]() 的一條切線交橢圓
的一條切線交橢圓![]() 于
于![]() ,
, ![]() 兩點,求
兩點,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某項科研活動共進行了5次試驗,其數據如下表所示:
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
(1)從5次特征量![]() 的試驗數據中隨機地抽取兩個數據,求至少有一個大于600的概率;
的試驗數據中隨機地抽取兩個數據,求至少有一個大于600的概率;
(2)求特征量![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;并預測當特征量
;并預測當特征量![]() 為570時特征量
為570時特征量![]() 的值.
的值.
(附:回歸直線的斜率和截距的最小二乘法估計公式分別為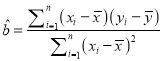 ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某手機生產企業為了解消費者對某款手機功能的認同情況,通過銷售部隨機抽取50名購買該款手機的消費者,并發出問卷調查(滿分50分),該問卷只有30份給予回復,這30份的評分如下:

(Ⅰ)完成下面的莖葉圖,并求16名男消費者評分的中位數與14名女消費者評分的平均值;
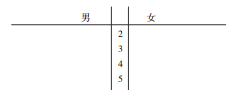

(Ⅱ)若大于40分為“滿意”,否則為“不滿意”,完成上面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為消費者對該款手機的“滿意度”與性別有關.
的把握認為消費者對該款手機的“滿意度”與性別有關.
參考公式:  ,其中
,其中![]()
參考數據:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,正方體ABCD-A1B1C1D1中,M、N分別是A1B1、B1C1的中點,問:

(1)AM和CN是否是異面直線?說明理由;
(2)D1B和CC1是否是異面直線?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 的展開式中第五項的系數與第三項的系數的比是10∶1.
的展開式中第五項的系數與第三項的系數的比是10∶1.
(1)求展開式中各項系數的和;
(2)求展開式中含![]() 的項;
的項;
(3)求展開式中系數最大的項和二項式系數最大的項.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com