
【題目】疫情過后,某商場開業一周累計生成2萬張購物單,從中隨機抽出100張,對每單消費金額進行統計得到下表:
消費金額(單位:元) |
|
|
|
|
|
購物單張數 | 25 | 25 | 30 | ? | ? |
由于工作人員失誤,后兩欄數據已無法辨識,但當時記錄表明,根據由以上數據繪制成的頻率分布直方圖所估計出的每單消費額的中位數與平均數恰好相等(用頻率估計概率),完成下列問題:
(1)估計該商場開業一周累計生成的購物單中,單筆消費額超過800元的購物單張數;
(2)為鼓勵顧客消費,拉動內需,該商場打算在今年國慶期間進行促銷活動,凡單筆消費超過600元者,可抽獎一次,中一等獎、二等獎、三等獎的顧客可以分別獲得價值![]() 元、
元、![]() 元、
元、![]() 元的獎品.已知中獎率為100%,且一等獎、二等獎、三等獎的中獎率依次構成等差數列,其中一等獎的中獎率為
元的獎品.已知中獎率為100%,且一等獎、二等獎、三等獎的中獎率依次構成等差數列,其中一等獎的中獎率為![]() .若今年國慶期間該商場的購物單數量預計比疫情后開業一周的購物單數量增長5%,試預測商場今年國慶期間采辦獎品的開銷.
.若今年國慶期間該商場的購物單數量預計比疫情后開業一周的購物單數量增長5%,試預測商場今年國慶期間采辦獎品的開銷.
【答案】(1)1000(張)(2)采購獎品的開銷可估計為![]() (元)
(元)
【解析】
(1)由中位數的定義,根據概率為![]() ,求得中位數,設消費在區間
,求得中位數,設消費在區間![]() 內的概率為
內的概率為![]() ,根據中位數與平均數恰好相等解得
,根據中位數與平均數恰好相等解得![]() 即可.
即可.
(2)根據中獎率為100%,且一等獎、二等獎、三等獎的中獎率依次構成等差數列,其中一等獎的中獎率為![]() ,設等差數列的公差為
,設等差數列的公差為![]() ,由
,由![]() ,解得
,解得![]() ,得到一等獎、二等獎、三等獎的中獎率,再根據購物單數量增長5%,得到今年的購物具有抽獎資格的單數,從而得到一等獎、二等獎、三等獎中獎單數,即可得到采購獎品的開銷.
,得到一等獎、二等獎、三等獎的中獎率,再根據購物單數量增長5%,得到今年的購物具有抽獎資格的單數,從而得到一等獎、二等獎、三等獎中獎單數,即可得到采購獎品的開銷.
(1)![]() ,
,
![]() 中位數為
中位數為![]() ,
,
又![]()
![]() 設消費在區間
設消費在區間![]() 內的概率為
內的概率為![]() ,
,
則消費在區間![]() 內的概率為
內的概率為![]()
由中位數與平均數恰好相等可知,![]() ,
,
解得![]() ,
,
故單筆消費超過800元的購物單張數為:![]() (張).
(張).
(2)設等差數列的公差為![]() ,
,
則![]() ,
,
解得![]() ,
,
故一等獎、二等獎、三等獎的中獎率分別為![]()
今年的購物具有抽獎資格的單數約為![]() ,
,
故一等獎、二等獎、三等獎中獎單數可估計為![]() ,
,
采購獎品的開銷可估計為![]() (元).
(元).


科目:高中數學 來源: 題型:
【題目】小張上班從家到公司開車有兩條線路,所需時間(分鐘)隨交通堵塞狀況有所變化,其概率分布如下表所示:
所需時間(分鐘) | 30 | 40 | 50 | 60 |
線路一 | 0.5 | 0.2 | 0.2 | 0.1 |
線路二 | 0.3 | 0.5 | 0.1 | 0.1 |
則下列說法正確的是( )
A.任選一條線路,“所需時間小于50分鐘”與“所需時間為60分鐘”是對立事件
B.從所需的平均時間看,線路一比線路二更節省時間
C.如果要求在45分鐘以內從家趕到公司,小張應該走線路一
D.若小張上、下班走不同線路,則所需時間之和大于100分鐘的概率為0.04
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國南宋數學家楊輝1261年所著的《詳解九章算法》一書里出現了如圖所示的表,即楊輝三角,這是數學史上的一個偉大成就.在“楊輝三角”中,第![]() 行的所有數字之和為
行的所有數字之和為![]() ,若去除所有為1的項,依次構成數列
,若去除所有為1的項,依次構成數列![]() ,則此數列的前55項和為( )
,則此數列的前55項和為( )

A. 4072B. 2026C. 4096D. 2048
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以原點為極點,
中,以原點為極點,![]() 軸正半軸為極軸建立極坐標系.已知曲線
軸正半軸為極軸建立極坐標系.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).
為參數).
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,已知點
兩點,已知點![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據閱兵領導小組辦公室介紹,2019年國慶70周年閱兵有59個方(梯)隊和聯合軍樂團,總規模約1.5萬人,是近幾次閱兵中規模最大的一次.其中,徒步方隊15個.為了保證閱兵式時隊列保持整齊,各個方隊對受閱隊員的身高也有著非常嚴格的限制,太高或太矮都不行.徒步方隊隊員,男性身高普遍在175cm至185cm之間;女性身高普遍在163cm至175cm之間,這是常規標準.要求最為嚴格的三軍儀仗隊,其隊員的身高一般都在184cm至190cm之間.經過隨機調查某個閱兵陣營中女子100人,得到她們身高的直方圖,如圖,記C為事件:“某一閱兵女子身高不低于169cm”,根據直方圖得到P(C)的估計值為0.5.

(1)求直方圖中a,b的值;
(2)估計這個陣營女子身高的平均值 (同一組中的數據用該組區間的中點值為代表)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線E的參數方程為![]() (
(![]() 為參數),以O為極點,x軸非負半軸為極軸建立極坐標系,直線
為參數),以O為極點,x軸非負半軸為極軸建立極坐標系,直線![]() ,
,![]() 的極坐標方程分別為
的極坐標方程分別為![]() ,
,![]() ,
,![]() 交曲線E于點A,B,
交曲線E于點A,B,![]() 交曲線E于點C,D.
交曲線E于點C,D.
(1)求曲線E的普通方程及極坐標方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】區塊鏈技術被認為是繼蒸汽機、電力、互聯網之后,下一代顛覆性的核心技術區塊鏈作為構造信任的機器,將可能徹底改變整個人類社會價值傳遞的方式,2015年至2019年五年期間,中國的區塊鏈企業數量逐年增長,居世界前列現收集我國近5年區塊鏈企業總數量相關數據,如表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
編號 | 1 | 2 | 3 | 4 | 5 |
企業總數量y(單位:千個) | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
注:參考數據![]() (其中z=lny).
(其中z=lny).
附:樣本(xi,yi)(i=1,2,…,n)的最小二乘法估計公式為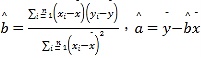
(1)根據表中數據判斷,y=a+bx與y=cedx(其中e=2.71828…,為自然對數的底數),哪一個回歸方程類型適宜預測未來幾年我國區塊鏈企業總數量?(給出結果即可,不必說明理由)
(2)根據(1)的結果,求y關于x的回歸方程(結果精確到小數點后第三位);
(3)為了促進公司間的合作與發展,區塊鏈聯合總部決定進行一次信息化技術比賽,邀請甲、乙、丙三家區塊鏈公司參賽比賽規則如下:①每場比賽有兩個公司參加,并決出勝負;②每場比賽獲勝的公司與未參加此場比賽的公司進行下一場的比賽;③在比賽中,若有一個公司首先獲勝兩場,則本次比賽結束,該公司就獲得此次信息化比賽的“優勝公司”,已知在每場比賽中,甲勝乙的概率為![]() ,甲勝丙的概率為
,甲勝丙的概率為![]() ,乙勝丙的概率為
,乙勝丙的概率為![]() ,請通過計算說明,哪兩個公司進行首場比賽時,甲公司獲得“優勝公司”的概率最大?
,請通過計算說明,哪兩個公司進行首場比賽時,甲公司獲得“優勝公司”的概率最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在邊長為4的菱形![]() 中,
中,![]() ,
,![]() 于點
于點![]() ,將
,將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如圖2.
,如圖2.

(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)判斷在線段![]() 上是否存在一點
上是否存在一點![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com