
【題目】探究函數![]() 的圖像時,列表如下:
的圖像時,列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
觀察表中y值隨x值的變化情況,完成以下的問題:
(1)函數![]() 的遞減區間是 ,遞增區間是 ;
的遞減區間是 ,遞增區間是 ;
(2)若對任意的![]() 恒成立,試求實數m的取值范圍.
恒成立,試求實數m的取值范圍.
科目:高中數學 來源: 題型:
【題目】下列說法中正確的個數是( )
(1) 已知![]() ,
,![]() ,
,![]() ,則
,則![]()
(2)將6個相同的小球放入4個不同的盒子中,要求不出現空盒,共有10種放法.
(3) ![]() 被
被![]() 除后的余數為
除后的余數為![]() .
.
(4) 若![]() ,則
,則![]() =
=![]()
(5)拋擲兩個骰子,取其中一個的點數為點![]() 的橫坐標,另一個的點數為點
的橫坐標,另一個的點數為點![]() 的縱坐標,連續拋擲這兩個骰子三次,點
的縱坐標,連續拋擲這兩個骰子三次,點![]() 在圓
在圓![]() 內的次數
內的次數![]() 的均值為
的均值為![]()
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知由實數構成的等比數列{an}滿足a1=2,a1+ a3+ a5=42.
(I)求數列{an}的通項公式;
(II)求a2+ a4+ a6+…+ a2n.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)令![]() ,試討論
,試討論![]() 的單調性;
的單調性;
(2)若對![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)由![]() ,對函數求導,研究導函數的正負得到單調性即可;(2)由條件可知
,對函數求導,研究導函數的正負得到單調性即可;(2)由條件可知![]() 對
對![]() 恒成立,變量分離
恒成立,變量分離![]() ,令
,令![]() ,求這個函數的最值即可.
,求這個函數的最值即可.
解析:
(1)由![]() 得
得![]()
當![]() 時,
時, ![]() 恒成立,則
恒成立,則![]() 單調遞減;
單調遞減;
當![]() 時,
時,  ,令
,令 ,
,
令 .
.
綜上:當![]() 時,
時, ![]() 單調遞減,無增區間;
單調遞減,無增區間;
當![]() 時,
時,  ,
, 
(2)由條件可知![]() 對
對![]() 恒成立,則
恒成立,則
當![]() 時,
時, ![]() 對
對![]() 恒成立
恒成立
當![]() 時,由
時,由![]() 得
得![]() .令
.令![]() 則
則
 ,因為
,因為![]() ,所以
,所以![]() ,即
,即![]()
所以![]() ,從而可知
,從而可知![]() .
.
綜上所述: 所求![]() .
.
點睛:導數問題經常會遇見恒成立的問題:
(1)根據參變分離,轉化為不含參數的函數的最值問題;
(2)若 ![]() 就可討論參數不同取值下的函數的單調性和極值以及最值,最終轉化為
就可討論參數不同取值下的函數的單調性和極值以及最值,最終轉化為![]() ,若
,若![]() 恒成立
恒成立![]() ;
;
(3)若![]() 恒成立,可轉化為
恒成立,可轉化為![]() (需在同一處取得最值) .
(需在同一處取得最值) .
【題型】解答題
【結束】
22
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以
為參數),以![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸的極坐標系中,直線
軸的非負半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·紹興仿真考試)已知數列{an}的奇數項依次構成公差為d1的等差數列,偶數項依次構成公差為d2的等差數列(其中d1,d2為整數),且對任意n∈N*,都有an<an+1,若a1=1,a2=2,且數列{an}的前10項和S10=75,則d1=________,a8=________.
查看答案和解析>>
科目:高中數學 來源: 題型:
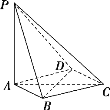
【題目】如圖,在四棱錐PABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
(1)求證:BD⊥平面PAC;
(2)若PA=4,求平面PBC與平面PDC所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是一個以A1B1C1為底面的直三棱柱被一平面所截得到的幾何體,截面為ABC,已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2,求:

(1)該幾何體的體積.
(2)截面ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C對應的邊分別是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面積S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com