
已知拋物線 的頂點為原點,其焦點
的頂點為原點,其焦點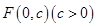 到直線
到直線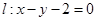 的距離為
的距離為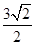 .設
.設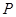 為直線
為直線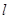 上的點,過點
上的點,過點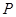 作拋物線
作拋物線 的兩條切線
的兩條切線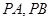 ,其中
,其中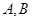 為切點.
為切點.
(Ⅰ)求拋物線 的方程;
的方程;
(Ⅱ)設點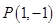 為直線
為直線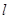 上的點,求直線
上的點,求直線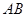 的方程;
的方程;
(Ⅲ) 當點 在直線
在直線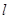 上移動時,求
上移動時,求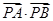 的最小值.
的最小值.
(1) 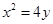 (2)
(2) 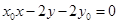 (3)
(3) 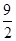
解析試題分析: (1)利用點到直線的距離公式直接求解C的值,便可確定拋物線方程;(2)利用求導的思路確定拋物線的兩條切線,借助均過點P,得到直線方程;(3)通過直線與拋物線聯立,借助韋達定理將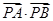 進行轉化處理,通過參數的消減得到函數關系式
進行轉化處理,通過參數的消減得到函數關系式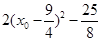 是解題的關鍵,然后利用二次函數求最值,需注意變量的范圍.
是解題的關鍵,然后利用二次函數求最值,需注意變量的范圍.
試題解析:(1)依題意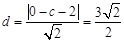 ,解得
,解得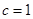 (負根舍去) (2分)
(負根舍去) (2分) 拋物線
拋物線 的方程為
的方程為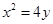 ; (4分)
; (4分)
(2)設點 ,
,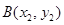 ,由
,由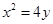 ,即
,即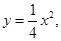 得
得
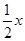 .
.
∴拋物線 在點
在點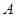 處的切線
處的切線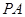 的方程為
的方程為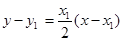 ,即
,即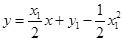 . (5分)
. (5分)
因為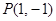 在切線
在切線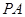 上且
上且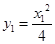 所以
所以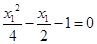 ,
,
從而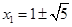 同理,
同理,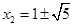 , (6分)
, (6分)
不妨取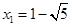 ,
,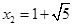 所以
所以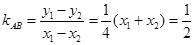 , (7分)
, (7分)
又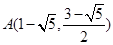 ,∴直線
,∴直線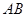 的方程為
的方程為 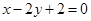 (8分)
(8分)
(3)依據(2)由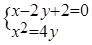 得,
得,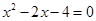 (9分)
(9分)
于是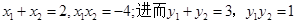 , (10分)
, (10分)
所以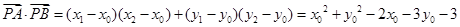
又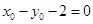 ,所以
,所以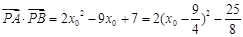 , (11分)
, (11分)
從而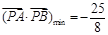 (12分)
(12分)
考點:拋物線的方程、定義、切線方程以及直線與拋物線的位置關系.


科目:高中數學 來源: 題型:解答題
如圖所示,已知圓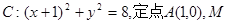 為圓上一動點,點
為圓上一動點,點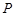 是線段
是線段 的垂直平分線與直線
的垂直平分線與直線 的交點.
的交點.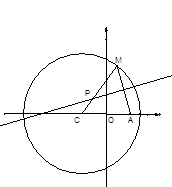
(1)求點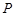 的軌跡曲線
的軌跡曲線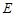 的方程;
的方程;
(2)設點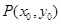 是曲線
是曲線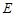 上任意一點,寫出曲線
上任意一點,寫出曲線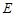 在點
在點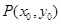 處的切線
處的切線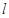 的方程;(不要求證明)
的方程;(不要求證明)
(3)直線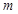 過切點
過切點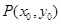 與直線
與直線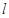 垂直,點
垂直,點 關于直線
關于直線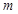 的對稱點為
的對稱點為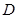 ,證明:直線
,證明:直線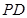 恒過一定點,并求定點的坐標.
恒過一定點,并求定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
矩形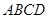 的中心在坐標原點,邊
的中心在坐標原點,邊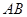 與
與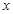 軸平行,
軸平行,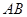 =8,
=8,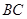 =6.
=6.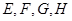 分別是矩形四條邊的中點,
分別是矩形四條邊的中點,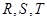 是線段
是線段 的四等分點,
的四等分點,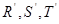 是線段
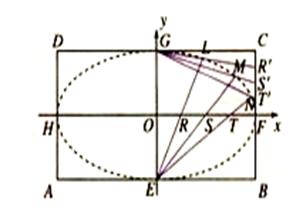
是線段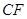 的四等分點.設直線
的四等分點.設直線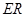 與
與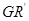 ,
,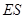 與
與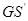 ,
,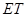 與
與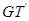 的交點依次為
的交點依次為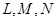 .
.
(1)以 為長軸,以
為長軸,以 為短軸的橢圓Q的方程;
為短軸的橢圓Q的方程;
(2)根據條件可判定點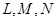 都在(1)中的橢圓Q上,請以點L為例,給出證明(即證明點L在橢圓Q上).
都在(1)中的橢圓Q上,請以點L為例,給出證明(即證明點L在橢圓Q上).
(3)設線段 的
的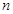 (
(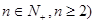 等分點從左向右依次為
等分點從左向右依次為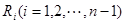 ,線段
,線段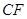 的
的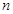 等分點從上向下依次為
等分點從上向下依次為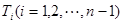 ,那么直線
,那么直線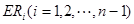 與哪條直線的交點一定在橢圓Q上?(寫出結果即可,此問不要求證明)
與哪條直線的交點一定在橢圓Q上?(寫出結果即可,此問不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,F1,F2分別是橢圓C: +
+ =1(a>b>0)的左、右焦點,A是橢圓C的頂點,B是直線AF2與橢圓C的另一個交點,∠F1AF2=60°
=1(a>b>0)的左、右焦點,A是橢圓C的頂點,B是直線AF2與橢圓C的另一個交點,∠F1AF2=60°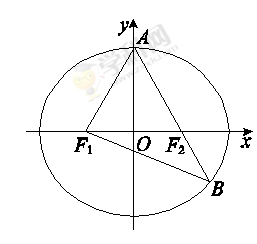
(1)求橢圓C的離心率;
(2)已知△AF1B的面積為40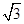 ,求a,b的值
,求a,b的值
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,斜率為 的直線過拋物線
的直線過拋物線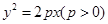 的焦點,與拋物線交于兩點A、B, M為拋物線弧AB上的動點.
的焦點,與拋物線交于兩點A、B, M為拋物線弧AB上的動點.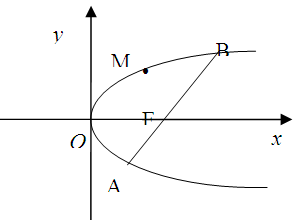
(Ⅰ).若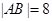 ,求拋物線的方程;
,求拋物線的方程;
(Ⅱ).求△ABM面積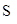 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在直角坐標系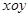 上取兩個定點
上取兩個定點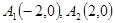 ,再取兩個動點
,再取兩個動點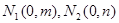 且
且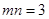 .
.
(I)求直線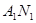 與
與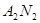 交點的軌跡
交點的軌跡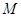 的方程;
的方程;
(II)已知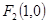 ,設直線:
,設直線: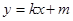 與(I)中的軌跡
與(I)中的軌跡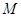 交于
交于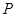 、
、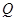 兩點,直線
兩點,直線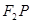 、
、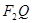 的傾斜角分別為
的傾斜角分別為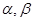 且
且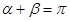 ,求證:直線過定點,并求該定點的坐標.
,求證:直線過定點,并求該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某跳水運動員在一次跳水訓練時的跳水曲線為如圖所示的拋物線一段,已知跳水板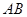 長為2m,跳水板距水面
長為2m,跳水板距水面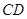 的高
的高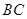 為3m,
為3m, =5m,
=5m,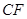 =6m,為安全和空中姿態優美,訓練時跳水曲線應在離起跳點
=6m,為安全和空中姿態優美,訓練時跳水曲線應在離起跳點 m(
m(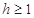 )時達到距水面最大高度4m,規定:以
)時達到距水面最大高度4m,規定:以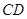 為橫軸,
為橫軸,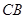 為縱軸建立直角坐標系.
為縱軸建立直角坐標系.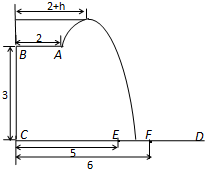
(1)當 =1時,求跳水曲線所在的拋物線方程;
=1時,求跳水曲線所在的拋物線方程;
(2)若跳水運動員在區域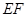 內入水時才能達到壓水花的訓練要求,求達到壓水花的訓練要求時
內入水時才能達到壓水花的訓練要求,求達到壓水花的訓練要求時 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com