
【題目】已知函數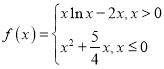 的圖象上有且僅有兩個不同的點關于直線
的圖象上有且僅有兩個不同的點關于直線![]() 的對稱點在
的對稱點在![]() 的圖象上,則實數
的圖象上,則實數![]() 的取值范圍是________.
的取值范圍是________.
【答案】![]()
【解析】
求出直線![]() 關于直線
關于直線![]() 對稱的直線
對稱的直線![]() 的方程
的方程![]() ,然后將問題轉化為直線
,然后將問題轉化為直線![]() 與函數
與函數![]() 的圖象有兩個交點,構造函數
的圖象有兩個交點,構造函數 ,將問題轉化為直線
,將問題轉化為直線![]() 與函數
與函數![]() 的圖象有兩個交點,利用數形結合思想可求出實數
的圖象有兩個交點,利用數形結合思想可求出實數![]() 的取值范圍.
的取值范圍.
直線![]() 關于直線
關于直線![]() 對稱的直線
對稱的直線![]() 的方程為
的方程為![]() ,即
,即![]() ,對應的函數為
,對應的函數為![]() .
.
所以,直線![]() 與函數
與函數![]() 的圖象有兩個交點.
的圖象有兩個交點.
對于一次函數![]() ,當
,當![]() 時,
時,![]() ,且
,且![]() .
.
則直線![]() 與函數
與函數![]() 的圖象交點的橫坐標不可能為
的圖象交點的橫坐標不可能為![]() .
.
當![]() 時,令
時,令![]() ,可得
,可得![]() ,
,
此時,令 .
.
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
此時,函數![]() 在區間
在區間![]() 上單調遞減,在區間
上單調遞減,在區間![]() 上單調遞增,
上單調遞增,
函數![]() 的極小值為
的極小值為![]() ;
;
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
此時,函數![]() 在區間
在區間![]() 上單調遞增,在區間
上單調遞增,在區間![]() 上單調遞減,
上單調遞減,
函數![]() 的極大值為
的極大值為![]() .
.
作出函數![]() 和函數
和函數![]() 的圖象如下圖所示:
的圖象如下圖所示:
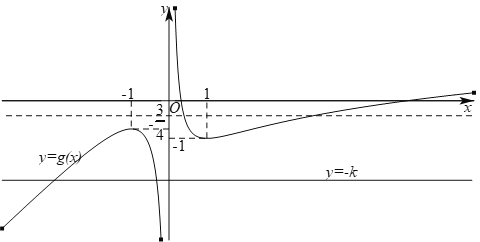
由圖象可知,當![]() 或
或![]() 時,即當
時,即當![]() 或
或![]() 時,直線
時,直線![]() 與函數
與函數![]() 的圖象有兩個交點.
的圖象有兩個交點.
因此,實數![]() 的取值范圍是
的取值范圍是![]() .
.
故答案為:![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 的部分圖像如圖所示,
的部分圖像如圖所示,![]() 兩點之間的距離為10,且
兩點之間的距離為10,且![]() ,若將函數
,若將函數![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度后所得函數圖像關于
個單位長度后所得函數圖像關于![]() 軸對稱,則
軸對稱,則![]() 的最小值為( )
的最小值為( )
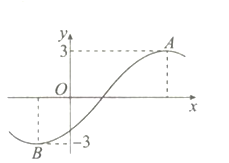
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】德國數學家萊布尼茲于1674年得到了第一個關于π的級數展開式,該公式于明朝初年傳入我國.我國數學家、天文學家明安圖為提高我國的數學研究水平,從乾隆初年(1736年)開始,歷時近30年,證明了包括這個公式在內的三個公式,同時求得了展開三角函數和反三角函數的6個新級數公式,著有《割圓密率捷法》一書,為我國用級數計算![]() 開創先河,如圖所示的程序框圖可以用萊布尼茲“關于
開創先河,如圖所示的程序框圖可以用萊布尼茲“關于![]() 的級數展開式計算
的級數展開式計算![]() 的近似值(其中P表示
的近似值(其中P表示![]() 的近似值)”.若輸入
的近似值)”.若輸入![]() ,輸出的結果P可以表示為( )
,輸出的結果P可以表示為( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,點
,點![]() 是橢圓上一點,
是橢圓上一點,![]() 是
是![]() 和
和![]() 的等差中項.
的等差中項.
(Ⅰ)求橢圓的標準方程;
(Ⅱ)若![]() 為橢圓的右頂點,直線
為橢圓的右頂點,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 的另一直線與橢圓交于
的另一直線與橢圓交于![]() 、
、![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知無窮數列![]() 的前
的前![]() 項中的最大項為
項中的最大項為![]() ,最小項為
,最小項為![]() ,設
,設![]() .
.
(1)若![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若數列![]() 是等差數列,求證:數列
是等差數列,求證:數列![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過拋物線![]() 焦點
焦點![]() 且傾斜角的
且傾斜角的![]() 直線
直線![]() 與拋物線
與拋物線![]() 交于點
交于點![]()
![]() 的面積為
的面積為![]() .
.
(I)求拋物線![]() 的方程;
的方程;
(II)設![]() 是直線
是直線![]() 上的一個動點,過
上的一個動點,過![]() 作拋物線
作拋物線![]() 的切線,切點分別為
的切線,切點分別為![]() 直線
直線![]() 與直線
與直線![]() 軸的交點分別為
軸的交點分別為![]() 點
點![]() 是以
是以![]() 為圓心
為圓心![]() 為半徑的圓上任意兩點,求
為半徑的圓上任意兩點,求![]() 最大時點
最大時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() ,
,![]() 點又恰為拋物線
點又恰為拋物線![]() 的焦點,以
的焦點,以![]() 為直徑的圓與橢圓
為直徑的圓與橢圓![]() 僅有兩個公共點.
僅有兩個公共點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點,記點
兩點,記點![]() ,
,![]() 到直線
到直線![]() 的距離分別為
的距離分別為![]() ,
,![]() ,
,![]() .直線
.直線![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點,記
兩點,記![]() ,
,![]() 的面積分別為
的面積分別為![]() ,
,![]() .
.
(ⅰ)證明:![]() 的周長為定值;
的周長為定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f (x)=ax﹣ex(a∈R),g(x)=![]() .
.
(Ⅰ)求函數f (x)的單調區間;
(Ⅱ)x0∈(0,+∞),使不等式f (x)≤g(x)﹣ex成立,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com