
已知:a=(cosa ,sina ),b=(cosb ,sinb )(0<a <b <p ),
(1)求證:a+b與a-b互相垂直;
(2)若ka+b與a-kb長度相等(其中k為非零實數),求b -a 的值.
|
(1)證法1:∵a=(cosa ,sina ),b=(cosb ,sinb ), ∴(a+b)=(cosa +cosb ,sina +sinb ), (a-b)=(cosa -cosb ,sina -sinb ). 又(a-b)·(a-b) =(cosa -cosb )(cosa -cosb )+(sina +sinb )(sina -sinb )
∴ (a+b)⊥(a-b).證法 2:∵a=(cosa ,sina ),b=(cosb ,sinb ),∴ 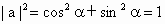 , ,
∴ ∴ ∴(a+b)⊥(a-b). (2)解法1:∵ka+b=(kcosa ,ksina )+(cosb ,sinb ) =(kcosa +cosb ,ksina +sinb ), a-kb=(cosa -kcosb ,sina -ksinb ), ∴
(注:cosa ·cosb +sina ·sinb =cos(a -b )) 同理可求 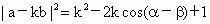 . .
又∵ |ka+b|=|a-kb|,∴ 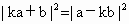 . .
∴ 2kcos(a -b )=-2kcos(a -b ).∵ k≠0,∴cos(a -b )=0.∴cos(b -a )=0.又∵ 0<a <b <p ,∴ . .
解法 2:∵|ka+b|=|a-kb|,∴ 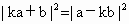
∴ 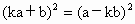 . .
∴ 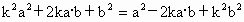 . .
又∵ 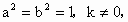 ∴a·b=0, ∴a·b=0,
∴ cosa cosb +sina sinb =0,∴cos(a -b )=0.∵ 0<a <b <p ,∴0<b -a <p ,∴ . .
|
|
本題中 (2)先對式子平方化簡更加簡單,在解題中要注意選擇本例中的兩種思路.(1)利用向量垂直坐標形式的充要條件證明; (2)利用長度公式,得出b -a 的三角函數值. |


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com