
已知四面體OABC中,OA、OB、OC兩兩相互垂直,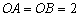 ,
,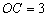 ,D為四面體OABC外一點.給出下列命題:①不存在點D,使四面體ABCD有三個面是直角三角形;②不存在點D,使四面體ABCD是正三棱錐;③存在點D,使CD與AB垂直并相等;④存在無數個點D,使點O在四面體ABCD的外接球面上.則其中正確命題的序號是( )
,D為四面體OABC外一點.給出下列命題:①不存在點D,使四面體ABCD有三個面是直角三角形;②不存在點D,使四面體ABCD是正三棱錐;③存在點D,使CD與AB垂直并相等;④存在無數個點D,使點O在四面體ABCD的外接球面上.則其中正確命題的序號是( )
A.①② B.②③ C.①③ D.③④
D
【解析】
試題分析:
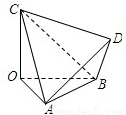
對于①,∵四面體OABC的三條棱OA,OB,OC兩兩垂直,OA=OB=2,OC=3,∴AC=BC=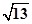 ,AB=2
,AB=2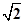 ,當四棱錐CABD與四面體OABC一樣時,即取CD=3,AD=BD=2,四面體ABCD的三條棱DA、DB、DC兩兩垂直,此時點D,使四面體ABCD有三個面是直角三角形,故①不正確;對于②,由①知AC=BC=
,當四棱錐CABD與四面體OABC一樣時,即取CD=3,AD=BD=2,四面體ABCD的三條棱DA、DB、DC兩兩垂直,此時點D,使四面體ABCD有三個面是直角三角形,故①不正確;對于②,由①知AC=BC=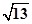 ,AB=2
,AB=2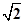 ,使AB=AD=BD,此時存在點D,CD=
,使AB=AD=BD,此時存在點D,CD=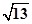 ,使四面體C-ABD是正三棱錐,故②不正確;對于③,取CD=AB,AD=BD,此時CD垂直面ABD,即存在點D,使CD與AB垂直并且相等,故③正確;對于④,先找到四面體OABC的內接球的球心P,使半徑為r,只需PD=r即可,∴存在無數個點D,使點O在四面體ABCD的外接球面上,故④正確,故正確的命題有③④,故選D.
,使四面體C-ABD是正三棱錐,故②不正確;對于③,取CD=AB,AD=BD,此時CD垂直面ABD,即存在點D,使CD與AB垂直并且相等,故③正確;對于④,先找到四面體OABC的內接球的球心P,使半徑為r,只需PD=r即可,∴存在無數個點D,使點O在四面體ABCD的外接球面上,故④正確,故正確的命題有③④,故選D.
考點:本題考查了空間中的線面關系
點評:本題考查棱錐的結構特征,同時考查了空間想象能力,轉化與劃歸的思想,以及構造法的運用,屬于中檔題


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
已知四面體OABC中,OA、OB、OC兩兩相互垂直,![]() ,
,![]() ,D為四面體OABC外一點.給出下列命題:①不存在點D,使四面體ABCD有三個面是直角三角形;②不存在點D,使四面體ABCD是正三棱錐;③存在點D,使CD與AB垂直并相等;④存在無數個點D,使點O在四面體ABCD的外接球面上.則其中正確命題的序號是( )
,D為四面體OABC外一點.給出下列命題:①不存在點D,使四面體ABCD有三個面是直角三角形;②不存在點D,使四面體ABCD是正三棱錐;③存在點D,使CD與AB垂直并相等;④存在無數個點D,使點O在四面體ABCD的外接球面上.則其中正確命題的序號是( )
A.①② B.②③ C.①③ D.③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com