
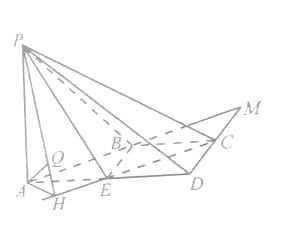
【題目】如圖,在四棱錐P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.

(I)在平面PAB內找一點M,使得直線CM∥平面PBE,并說明理由;
(II)若二面角P-CD-A的大小為45°,求直線PA與平面PCE所成角的正弦值.
【答案】(Ⅰ)見解析;(Ⅱ)![]() .
.
【解析】試題分析:本題考查線面平行、線線平行、向量法等基礎知識,考查空間想象能力、分析問題的能力、計算能力.第一問,利用線面平行的定理,先證明線線平行,再證明線面平行;第二問,可以先找到線面角,再在三角形中解出正弦值,還可以用向量法建立直角坐標系解出正弦值.
試題解析:(Ⅰ)在梯形ABCD中,AB與CD不平行.
延長AB,DC,相交于點M(M∈平面PAB),點M即為所求的一個點.理由如下:
由已知,BC∥ED,且BC=ED.
所以四邊形BCDE是平行四邊形.
從而CM∥EB.
又EB![]() 平面PBE,CM
平面PBE,CM![]() 平面PBE,
平面PBE,
所以CM∥平面PBE.
(說明:延長AP至點N,使得AP=PN,則所找的點可以是直線MN上任意一點)
(Ⅱ)方法一:
由已知,CD⊥PA,CD⊥AD,PA![]() AD=A,
AD=A,
所以CD⊥平面PAD.
從而CD⊥PD.
所以![]() PDA是二面角P-CD-A的平面角.
PDA是二面角P-CD-A的平面角.
所以![]() PDA=45°.
PDA=45°.
設BC=1,則在Rt△PAD中,PA=AD=2.
過點A作AH⊥CE,交CE的延長線于點H,連接PH.
易知PA⊥平面ABCD,
從而PA⊥CE.
于是CE⊥平面PAH.
所以平面PCE⊥平面PAH.
過A作AQ⊥PH于Q,則AQ⊥平面PCE.
所以![]() APH是PA與平面PCE所成的角.
APH是PA與平面PCE所成的角.
在Rt△AEH中,![]() AEH=45°,AE=1,
AEH=45°,AE=1,
所以AH=![]() .
.
在Rt△PAH中,PH=![]() =
=![]() ,
,
所以sin![]() APH=
APH=![]() =
=![]() .
.
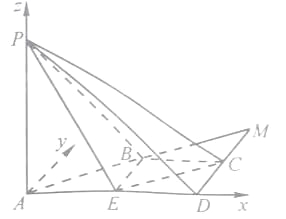
方法二:
由已知,CD⊥PA,CD⊥AD,PA![]() AD=A,
AD=A,
所以CD⊥平面PAD.
于是CD⊥PD.
從而![]() PDA是二面角P-CD-A的平面角.
PDA是二面角P-CD-A的平面角.
所以![]() PDA=45°.
PDA=45°.
由PA⊥AB,可得PA⊥平面ABCD.
設BC=1,則在Rt△PAD中,PA=AD=2.
作Ay⊥AD,以A為原點,以![]() ,
,![]() 的方向分別為x軸,z軸的正方向,建立如圖所示的空間直角坐標系A-xyz,則A(0,0,0),P(0,0,2),C(2,1,0),E(1,0,0),
的方向分別為x軸,z軸的正方向,建立如圖所示的空間直角坐標系A-xyz,則A(0,0,0),P(0,0,2),C(2,1,0),E(1,0,0),
所以![]() =(1,0,-2),
=(1,0,-2),![]() =(1,1,0),
=(1,1,0),![]() =(0,0,2)
=(0,0,2)
設平面PCE的法向量為n=(x,y,z),
由 得
得![]() 設x=2,解得n=(2,-2,1).
設x=2,解得n=(2,-2,1).
設直線PA與平面PCE所成角為α,則sinα=![]() =
=![]() .
.
所以直線PA與平面PCE所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某大型超市在2018年元旦舉辦了一次抽獎活動,抽獎箱里放有3個紅球,3個黃球和1個藍球(這些小球除顏色外大小形狀完全相同),從中隨機一次性取3個小球,每位顧客每次抽完獎后將球放回抽獎箱.活動另附說明如下:
①凡購物滿100(含100)元者,憑購物打印憑條可獲得一次抽獎機會;
②凡購物滿188(含188)元者,憑購物打印憑條可獲得兩次抽獎機會;
③若取得的3個小球只有1種顏色,則該顧客中得一等獎,獎金是一個10元的紅包;
④若取得的3個小球有3種顏色,則該顧客中得二等獎,獎金是一個5元的紅包;
⑤若取得的3個小球只有2種顏色,則該顧客中得三等獎,獎金是一個2元的紅包.
抽獎活動的組織者記錄了該超市前20位顧客的購物消費數據(單位:元),繪制得到如圖所示的莖葉圖.

(1)求這20位顧客中獎得抽獎機會的顧客的購物消費數據的中位數與平均數(結果精確到整數部分);
(2)記一次抽獎獲得的紅包獎金數(單位:元)為![]() ,求
,求![]() 的分布列及數學期望,并計算這20位顧客(假定每位獲得抽獎機會的顧客都會去抽獎)在抽獎中獲得紅包的總獎金數的平均值.
的分布列及數學期望,并計算這20位顧客(假定每位獲得抽獎機會的顧客都會去抽獎)在抽獎中獲得紅包的總獎金數的平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點.
的左、右焦點.
(1)若![]() 是該橢圓上的一個動點,求
是該橢圓上的一個動點,求![]() 的最大值和最小值;
的最大值和最小值;
(2)設過定點![]() 的直線
的直線![]() 與橢圓交于不同的兩點
與橢圓交于不同的兩點![]() ,且
,且![]() 為銳角(其中
為銳角(其中![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校在2010年的自主招生考試成績中隨機抽取100名學生的筆試成績,按成績分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示。
,得到的頻率分布直方圖如圖所示。

(1)求第3、4、5組的頻率;
(2)為了能選拔出最優秀的學生,該校決定在筆試成績高的第3、4、5組中用分層抽樣的方法抽取6名學生進入第二輪面試,求第3、4、5組每組各抽取多少學生進入第二輪面試?
(3)在(2)的前提下,學校決定在這6名學生中隨機抽取2名學生接受甲考官的面試,求第4組至少有一名學生被甲考官面試的概率。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com