
(文科)(本題滿分14分)設函數f(x)= ·
· ,其中
,其中 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且函數y=f(x)的圖象經過點(
=(1+sin2x,1),x∈R,且函數y=f(x)的圖象經過點( ,2).
,2).
(Ⅰ)求實數m的值;
(Ⅱ)求函數f(x)的最小值及此時x值的集合
(理科)(本題滿分14分)已 知函數f(x)=ex-kx,x∈R
知函數f(x)=ex-kx,x∈R
(Ⅰ)若k=e,試確定函數f(x)的單調區間
(Ⅱ)若k>0,且對于任意x∈R,f(|x|)>0恒成立,試確定實數k的取值范圍
(文科)解:(Ⅰ)f(x)=a·b="m(1+sin2x)+cos2x."
由已知得f( )=m(1+sin
)=m(1+sin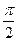 )+cos
)+cos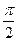 =2,解得m=1.……6分
=2,解得m=1.……6分
(Ⅱ)由(Ⅰ)得f( x)=1+sin2x+cos2x=1+
x)=1+sin2x+cos2x=1+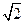 sin(2x+
sin(2x+ ).
).
所以當sin(2x+ )=-1時,f(x)的最小值為1-
)=-1時,f(x)的最小值為1-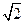 . ……………11分
. ……………11分
由sin(2x+ )=-1,得x值的集合為{x|x=k
)=-1,得x值的集合為{x|x=k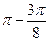 ,k∈Z}.……14分
,k∈Z}.……14分
(理科)解:(Ⅰ)由k=e得f(x)=ex-ex,所以f (x)=ex-e.
(x)=ex-e.
由f (x)>0得x>1,
(x)>0得x>1,
故f(x)的單調遞增區間是(1,+∞);……………………4分
由f (x)<0得x<1,
(x)<0得x<1,
故f(x)的單調遞減區間是(-∞,1). ……………………6分
(Ⅱ)由f(|-x|)=f(|x|)可知f(|x|)是偶函數. 于是 f(|x|)>0對任意x∈R成立等價于f(x)>0對任意x≥0成立. 由f
f(|x|)>0對任意x∈R成立等價于f(x)>0對任意x≥0成立. 由f (x)=ex-k=0得x="lnk."
(x)=ex-k=0得x="lnk."
①當k∈(0,1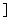 時,f
時,f (x)=ex-k>1-k≥0(x>0). 此時f(x)在[0,+∞
(x)=ex-k>1-k≥0(x>0). 此時f(x)在[0,+∞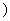 上單調遞增. 故f(x)≥f(0)=1>0,符合題意.所以0<k≤1. …………10分②當k∈(1,+∞)時,lnk>0. 當x變化時f
上單調遞增. 故f(x)≥f(0)=1>0,符合題意.所以0<k≤1. …………10分②當k∈(1,+∞)時,lnk>0. 當x變化時f (x),f(x)的變化情況如下
(x),f(x)的變化情況如下 :
:
由此可得,在[0,+∞x (0,lnk) lnk (lnk,+∞) f  (x)
(x)- 0 + f(x) 單調遞減 極小值 單調遞增 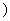 上,f(x)≥f(lnk)=k-klnk.
上,f(x)≥f(lnk)=k-klnk.
依題意,k-klnk>0. 又k>1,所以1<k<e.
綜合①②實數k的取值范圍為(0,e). …………………………14分
解析


 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案科目:高中數學 來源:2013屆四川省成都外國語學校高二下學期期中考試數學試卷(解析版) 題型:解答題
(本題滿分14分)已知函數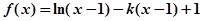 .
.
(1)求函數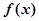 的單調區間;
的單調區間;
(2)若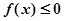 恒成立,求實數k的取值范圍;
恒成立,求實數k的取值范圍;
(文科(3)證明: 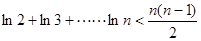
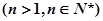 .
.
(理科(3)證明: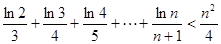
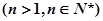 .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省高三上學期期中考試數學 題型:解答題
(文科)(本題滿分14分)設函數f(x)= ·
· ,其中
,其中 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且函數y=f(x)的圖象經過點(
=(1+sin2x,1),x∈R,且函數y=f(x)的圖象經過點(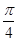 ,2).
,2).
(Ⅰ)求實數m的值;
(Ⅱ)求函數f(x)的最小值及此時x值的集合
(理科)(本題滿分14分)已知函數f(x)=ex-kx,x∈R
(Ⅰ)若k=e,試確定函數f(x)的單調區間
(Ⅱ)若k>0,且對于任意x∈R,f(|x|)>0恒成立,試確定實數k的取值范圍
查看答案和解析>>
科目:高中數學 來源:2010-2011年四川省成都市高二3月月考數學試卷 題型:填空題
(文科做)(本題滿分14分)如圖,在長方體
ABCD—A1B1C1D1中,AD=AA1=1,AB=2,點E在棱AB上移動.
(1)證明:D1E⊥A1D;
(2)當E為AB的中點時,求點E到面ACD1的距離;
(3)AE等于何值時,二面角D1—EC-D的大小為 .
.

(理科做)(本題滿分14分)
如圖,在直三棱柱ABC – A1B1C1中,∠ACB = 90°,CB = 1,
CA = ,AA1 =
,AA1 = ,M為側棱CC1上一點,AM⊥BA1.
,M為側棱CC1上一點,AM⊥BA1.
(Ⅰ)求證:AM⊥平面A1BC;
(Ⅱ)求二面角B – AM – C的大小;
(Ⅲ)求點C到平面ABM的距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
(文科)(本題滿分14分)設函數f(x)=![]() ·
·![]() ,其中
,其中![]() =(m,cos2x),
=(m,cos2x),![]() =(1+sin2x,1),x∈R,且函數y=f(x)的圖象經過點(
=(1+sin2x,1),x∈R,且函數y=f(x)的圖象經過點(![]() ,2).
,2).
(Ⅰ)求實數m的值;
(Ⅱ)求函數f(x)的最小值及此時x值的集合.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com