
【題目】解答題
(1)在等比數列{an}中,a5=162,公比q=3,前n項和Sn=242,求首項a1和項數n.
(2)有四個數,其中前三個數成等比數列,其積為216,后三個數成等差數列,其和為36,求這四個數.
【答案】
(1)解: 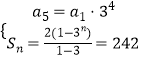
∴a1=2,n=5
(2)解:設這四個數分別為 ![]()
由題意 ![]() ,
,
∴a=6,q=2
∴四數為3、6、12、18
【解析】(1)利用數列的通項與前n項和公式建立方程組,即可求首項a1和項數n.(2)設這四個數分別為 ![]() ,根據條件建立方程組,即可求這四個數.
,根據條件建立方程組,即可求這四個數.
【考點精析】解答此題的關鍵在于理解等差數列的性質的相關知識,掌握在等差數列{an}中,從第2項起,每一項是它相鄰二項的等差中項;相隔等距離的項組成的數列是等差數列,以及對等比數列的基本性質的理解,了解{an}為等比數列,則下標成等差數列的對應項成等比數列;{an}既是等差數列又是等比數列== {an}是各項不為零的常數列.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+ ![]() .
.
(1)判斷f(x)的奇偶性并說明理由;
(2)當a=16時,判斷f(x)在x∈(0,2]上的單調性并用定義證明;
(3)試判斷方程x3﹣2016x+16=0在區間(0,+∞)上解的個數并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線y2=2px(p>0)的焦點為F,A(x1,y1),B(x2,y2)是過F的直線與拋物線的兩個交點,求證:
(1)y1y2=-p2,![]() ;(2)
;(2)![]() 為定值;
為定值;
(3)以AB為直徑的圓與拋物線的準線相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某房地產開發公司計劃在一樓區內建造一個長方形公園ABCD,公園由長方形的休閑區A1B1C1D1(陰影部分)和環公園人行道組成.已知休閑區A1B1C1D1的面積為4000平方米,人行道的寬分別為4米和10米. 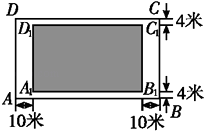
(1)若設休閑區的長A1B1=x米,求公園ABCD所占面積S關于x的函數S(x)的解析式;
(2)要使公園所占面積最小,休閑區A1B1C1D1的長和寬該如何設計?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() 在
在![]() 和
和![]() 處取得極值,且
處取得極值,且![]() ,曲線
,曲線![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 垂直.
垂直.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)證明關于![]() 的方程
的方程![]() 至多只有兩個實數根(其中
至多只有兩個實數根(其中![]() 是
是![]() 的導函數,
的導函數, ![]() 是自然對數的底數).
是自然對數的底數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】互不相等的三個正數x1 , x2 , x3成等比數列,且點P1(logax1 , logby1)P2(logax2 , logby2),P3(logax3 , logby3)共線(a>0且a≠0,b>且b≠1)則y1 , y2 , y3成( )
A.等差數列,但不等比數列
B.等比數列而非等差數列
C.等比數列,也可能成等差數列
D.既不是等比數列,又不是等差數列
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com