定義:若數列{An}滿足An+1=An2,則稱數列{An}為“平方遞推數列”.已知數列{an}中,a1=2,點(an,an+1)在函數f(x)=x2+4x+2的圖象上,其中n為正整數.
(1)判斷數列{an+2}是否為“平方遞推數列”?說明理由.
(2)證明數列{lg(an+2)}為等比數列,并求數列{an}的通項.
(3)設Tn=(2+a1)(2+a2)…(2+an),求Tn關于n的表達式.
【答案】
分析:(1)根據點(a
n,a
n+1)在函數f(x)=x
2+4x+2的圖象上,可以得到數列{a
n}的遞推關系式,再應用完全平方公式,就可得到數列{a
n+2}的遞推關系式,根據數列{a
n+2}的遞推關系式,可判斷是否為“平方遞推數列”.
(2)欲證明數列{lg(a
n+2)}為等比數列,只需證明此數列的后一項與前一項的比是常數,由(1)所得
a
n+1+2=(a
n+2)
2,兩邊取常用對數,即可證明.再利用等比數列通項公式求出數列{lg(a
n+2)}的通項公式,進而得到數列{a
n}的通項公式.
(3)由(2)可求數列{lg(a
n+2)}的通項公式,求出數列{lg(a
n+2)}的前n項和,再借助對數函數的運算律,求出lgT
n,把等式兩邊的對數符號去掉,即可得到T
n關于n的表達式.
解答:解:(1)由條件得:a
n+1=a
n2+4a
n+2,
∴a
n+1+2=a
n2+4a
n+4=(a
n+2)
2,∴{a
n+2}是“平方遞推數列”.
(2)由(1)得
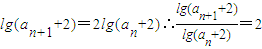
,
∴{lg(a
n+2)}為等比數列.
∵lg(a
1+2)=lg4,∴lg(a
n+2)=lg4•2
n-1,∴
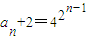
∴
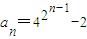
.
(3)∵
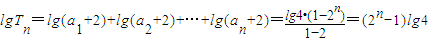
,
∴
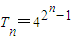
.
點評:本題主要考查了構造法判斷數列的性質以及求數列的通項公式,求和.屬于數列的綜合題.

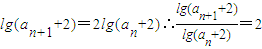 ,
,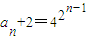
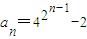 .
. 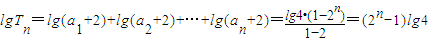 ,
,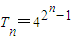 .
.

 閱讀快車系列答案
閱讀快車系列答案